1) 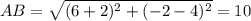
2) Составим уравнение АB:
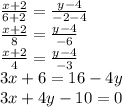
Это требуемое уравнение. Коэффициент АВ 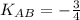
3) Составим уравнение ВС:
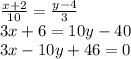
Это требуемое уравнение. Коэффициент BC 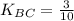
4) Пусть АМ-медиана. M- середина ВC

Составим уравнение AM:
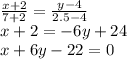
Это требуемое уравнение.
5) Пусть BN-медиана. N- середина AC
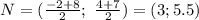
Составим уравнение BN:
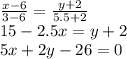
Это требуемое уравнение.
6) Пусть СК-высота к стороне АВ.
Тогда СК и АВ взаимно перпендикулярны, причем
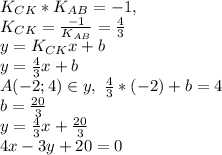
Это уравнение высоты СК.
7) Площадь треугольника АВС
![S_{ABC}=б\frac{1}{2}*|AB \times AC|=б\frac{1}{2}*\left[\begin{array}{ccc}-2-8&4-7\\6-8&-2-7\end{array}\right]= \\\ =б\frac{1}{2}*\left[\begin{array}{ccc}-10&-3\\-2&-9\end{array}\right]=\frac{1}{2}*(90-6)=42](/tpl/images/0172/4549/f35e9.png)
8) Пусть CF||AB, тогда 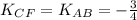
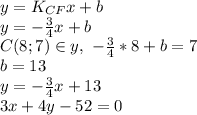 /
/
Это уравнение прямой CF||AB.
cos2x - V3*tgx*cos2x = 1 - V3*tgx
cos2x(1 - V3*tgx) - (1 - V3*tx) = 0
(1 - V3*tgx)*(cos2x - 1) = 0
1) случай. 1 - V3*tgx = 0 V3*tgx = 1 tgx = 1/V3 > x = pi/6 учитывая, что
надо выбрать наименьший положительный корень.
2) случай cos2x - 1 = 0 cos2x = 1 > 2x = 2*pi, x = pi учитывая, что
надо выбрать наименьший положительный корень.
Из двух корней выбираем наименьший положительный корень он будет равен pi/6.
ответ. pi/6
x; x+1; x+2; x+3
Условие: разность произведений равна 58:
(x+2)(x+3) - x(x+1) = 58
x^2 + 5x + 6 - x^2 - x = 58
4x = 58 - 6 = 52
x = 13
ответ: 13, 14, 15, 16.