Объяснение:
Решение.
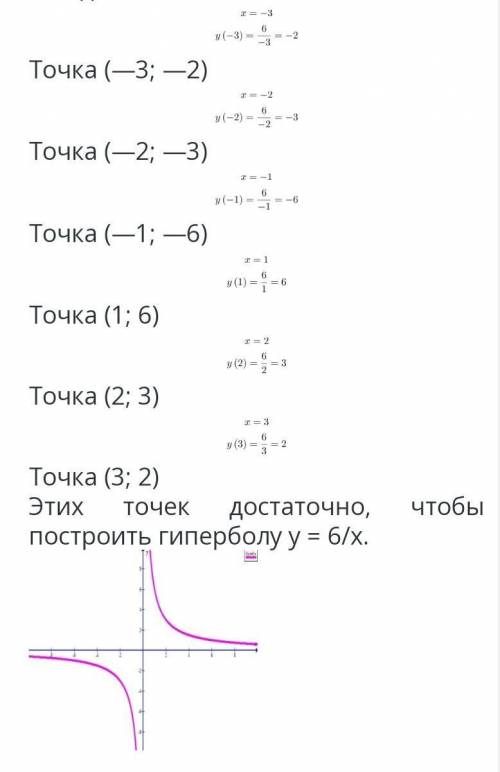
Разберем последовательно как можно просто и без ошибок построить график любой функции.
Для этого первым делом рассмотрим функцию, график которой нужно построить.
Данная функция представлена в виде дроби целого известного числа и неизвестного, причем неизвестное стоит в знаменателе дроби. Вспоминаем математику начальных классов, когда учили, что делить нельзя только на ноль. Из этого делаем вывод, что неизвестное число х для заданной функции может быть каким угодно, кроме нуля. Теперь можно записать область значений переменной х:
Проверим, является ли функция четной. Для этого подставим —х в ее уравнение вместо х и сделаем вывод:
Получаем нечетную функцию. Для нас такая информация полезна тем, что график нечетной функции симметричен началу координат, то есть точке (0; 0).
Найдем точки, которые принадлежат графику, чтобы провести через них кривую. Выберем точки произвольно и подставим вместо х:
Объяснение:
1) -y²+6y-12
вынесем минус за скобку
-y²+6y-12=-(y²-6y+12)
выделим в скобке полный квадрат, для этого добавим и отнимем 9
-y²+6y-12=-(y²-6y+12)=-(y²-6y+9-9+12)
По формуле сокращенного умножения y²-6y+9=(у-3)²
-y²+6y-12=-(y²-6y+12)=-(y²-6y+9-9+12)=-((у-3)²-9+12)=-((у-3)²+3)
так как (у-3)²≥0 и 3>0 то (у-3)²+3>0 ⇒
-((у-3)²+3)<0
так как -y²+6y-12=-((у-3)²+3) и -((у-3)²+3)<0
то -y²+6y-12<0
2) Другой
Графиком функции y=-x²+6x-12 является парабола
так как a=-1 то ветки направлены вниз
координата вершины x=-b/2a=-6/-2=3
y(3)=-9+18-12=-3
максимальное значение функции y=-x²+6x-12 это -3
⇒ -x²+6x-12≤-3
так как -3<0 то
-x²+6x-12<0
заменим х на у
получим
-y²+6y-12<0
Замечание
В условии задачи надо убрать =0
так как трехчлен принимает только отрицательные значения то он не может быть равен 0
По теореме Виета:
х1*х2= -6
х1+х2= 4,5
а) х1^2*х2+х1*х2^2= х1*х2(х1+х2)= -6*4,5= -27
б) х2/х1+х1/х2= (х2^2+х1^2)/х1*х2= ((х1+х2)^2- 2*х1*х2)/х1*х2= (4,5^2-2*(-6))/(-6)= (20,25+12)/(-6)= 32,25/6= 5,375
в) х1^3+х2^3= (х1+х2)((х1+х2)^2-3х1х2)= 4,5(20,25+18)= 172,125