Производная по определению - предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует.
Δy = f(x+Δx) - f(x) = √(1+2(x+Δx)) - √(1+2x) = √(1+2x+2Δx) - √(1+2x)
Преобразуем выражение, домножив числитель и знаменатель на сопряженное выражение:
(√(1+2x+2Δx) - √(1+2x))(√(1+2x+2Δx) + √(1+2x))/(√(1+2x+2Δx) + √(1+2x)) = (1+2x+2Δx - 1 -2x)/(√(1+2x+2Δx) + √(1+2x))= (2Δx)/(√(1+2x+2Δx) + √(1+2x))
Δy/Δx = 2/(√(1+2x+2Δx) + √(1+2x))
limΔx->0 (2/(√(1+2x+2Δx) + √(1+2x)) = 2/(√(1+2x) + √(1+2x)) = 2/(2√(1+2x) = 1/√(1+2x)
ответ: y' = 1/√(1+2x)
Не люблю задания, в которых больше одной задачи. Но эти задачи симпатичные, допускающие не совсем стандартные рассуждения. Вот ради этих рассуждений я и берусь за решение задач.
4. 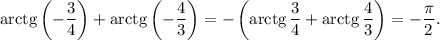 ответ: - 1
ответ: - 1
Объяснение: арктангенс трех четвертых и арктангенс четырех третьих - это острые углы в прямоугольном треугольнике с катетами 3 и 4, поэтому их сумма равна 90 градусам.
6. арктангенсы одной второй и одной третьей меньше 45 градусов, поэтому их сумма лежит в первой четверти. Воспользуемся формулой
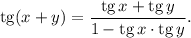
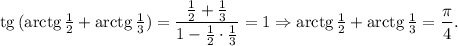
Осталось сосчитать синус полученного угла и возвести результат в квадрат. ответ: 0,5
5. Арксинус 4/5 - это острый угол (лежащий против катета, равного 4) прямоугольного треугольника ABC с катетами BC=4 и AC=3 и гипотенузой AB=5. Нас интересует половина этого угла, поэтому рисуем биссектрису AD , которая поделит катет BC на отрезки CD=3/2 и DB=5/2, пропорциональные боковым сторонам. В прямоугольном треугольнике ADC катеты AC=3; CD=3/2. Чтобы упростить вычисления, рассмотрим подобный ему треугольник A'D'C' с катетами A'C'=2 и C'D'=1 и гипотенузой A'D'=корень из 5. Интересующий нас угол, равный половине арксинуса 4/5 - это угол A' этого треугольника, а второй острый угол равен арктангенсу 2. Поэтому
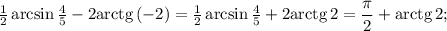
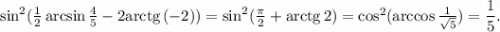
ответ: 0,2
Примем начальный вклад за х, а начисляемый процент за у, тогда можем момтавить систему уравнений:
Оставим в левой части каждого уравнения х:
Первое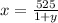
второе х*(1+2у)=540+200у
Уравняем правые части уравнений:
525*(1+2y)=(540+200y)*(1+y)
Находим корни квадратного уравнения. Получаем: у1=1,5 и у2=0,05
В случае у1=1.5 (или 150 % прибыли)
х=525/(1+у)=525/(1+1,5)=210 руб. - размер вклада
В случае у2=0,05 (или 5% прибыли)
х=525/(1+0,05)=500 руб. - размер вклада.
ответ: задача имеет два решения:
1) вклад 210 руб. под 150% годовых
2) вклад 500 руб под 5% годовых.