Объяснение:
1.
C⁵ₓ₊₁=(3/8)*A³ₓ
(x+1)!/((x+1-5)!*5!)=(3/8)*x!/(x-3)!
(x+1)!/((x-4)!*5!)=(3/8)*x!/((x-4)!(x-3))
x!*(x+1)/5!=(3/8)*x!/(x-3)
(x+1)/5!=(3/8)/(x-3)
(x-3)*(x+1)=(3/8)*120
x²-2x-3=45
x₂-2x-48=0 D=196 √D=14
x₁=-6 ∉ x₂=8.
ответ: х=8.
2.
Cˣ⁻⁴ₓ₊₁=(7/15)*A³ₓ₊₁
(x+1)!/((x+1-(x-4))!*(x-4)!=(7/15)*(x+1)!/(x+1-3)!
(x+1)!/(5!*(x-4)!=(7/15)*(x+1)!/(x-2)!
1/(5!*(x-4)!)=(7/15)/((x-4)!*(x-3)*(x-2))
1/5!=(7/15)/((x-3)*(x-2))
15*(x-3)*(x-2)=7*5!
15*(x²-5x+6)=7*120 |÷15
x²-5x+6=7*8
x²-5x+6=56
x²-5x-50=0 D=225 √D=15
x₁=-5 ∉ x₂=10.
ответ: х=10.
а) n-ый член геометрической прогрессии ищется по формуле:
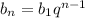
Тогда пятый член этой прогрессии равен:

б) Аналогично по формуле n-го члена геом. прогрессии вычисляем девятый член прогрессии:
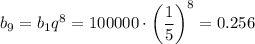
в) Сумма первых n членов геометрической прогрессии ищется по следующей формуле:
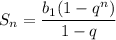
Тогда сумма первых восьми членов этой прогрессии равна:

г) Аналогично с в) по формуле суммы n первых членов геометрической прогрессии вычисляем сумму первых пяти членов этой прогрессии:
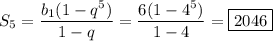
д) Предполагается, что нужно найти сумму бесконечно убывающей геометрической прогрессии:

Тогда
А) -36; - 12; -4;
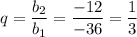
Сумма бесконечно уб. г.п. 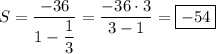
Б) 
Сумма бесконечно убывающей геометрической прогрессии:
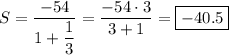
e) используя n-ый член геометрической прогрессии, рассмотрим пятый член этой прогрессии:
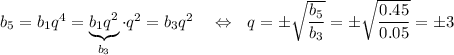
Так как по условию q>0, то q=3
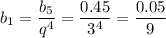
Сумма первых восьми членов этой прогрессии равна:

2) F`(x)=)cos(2x-4)+1)`=-2sin(2x-4)=d(x)