Відповідь: ( -1; 5 ; 1 ; 3)
( або в порядку зростання: (-1; 1; 3; 5)
Пояснення:
(х²-4х)²-2(х²-4х)-15=0;
1. (вираз (х²-4х)- замінемо на одну букву наприклад р и це запишемо)
Нехай (х²-4х)=р, тоді
( підставимо р в рівняння)
р²-2р-15=0.
2. Знайдемо дискримінант
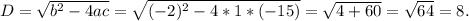
3.Знайдемо корні рівняння
р₁= (-b+D)/2a= (2+8)/2=10/2=5
р₂=(-b-D)/2a=(2-8)/2=-3
4) тепер підставляємо наше р₁ в рівняння (х²-4х)=р і рішаємо через дискримінант
(х²-4х)=5;
х²-4х-5=0
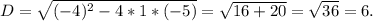
х₁=(-b-D)/2a=(4-6)/2=-1:
х₂=(-b+D)/2a=(4+6)/2=5;
5.тепер підставляємо наше р₂ в рівняння (х²-4х)=р і рішаємо через дискримінант
(х²-4х)=-3
х²-4х+3=0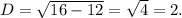
х₃=(-b-D)/2a=(4-2)/2=1:
х4=(-b+D)/2a=(4+2)/2=3;
Объяснение:
1) = (5х+3х-6)/15=(8х-6)/15
2) = (1+а^2-2a)/а^2 = (a-1)^2/а^2
3) =ab+b+a-ab / ab(a-b) = a+b/ ab(a-b)
4) = (4a*15b^2)/5b*2a^2=6b/a
5) = - (3а*в^3)/b^2*12a^2= - b/4a
6) = (3*2(x-2))/x (x-2)*x = 6/x^2
7) = (a-2b)*18c^2 / 12c * (-(a-2b)) = - 3c/2
8) = ((x^2+2x-5x)/(x+2)) : x-3/ x+2 = ( x (x-3)(x+2))/ (x+2) (x-3)= x
9) = ((a-x)(a+x)(b+4)/(b+4)(b-4)(a-x)) + 4/4-b = (a+x-4) / b-4
10) решаю по условию, что есть..
1) a^2+5a-a^2+5a+a+25 / (a-5)(a+5) = 11a+25 / (a-5)(a+5)
2) ( 11a+25 )* (a-5) / (a-5)(a+5)(a+5)^2 = 11a+25 / (a+5)^3
B) а 2а^b тут случаем а не в квадрате? если да то так:
.а^2(a-2b)-3b(a-2b)=(a-2b)(a^2-3b)