№ 1
а) Чтобы число принадлежало пересечению множеств А и В, оно должно принадлежать и множеству А, и множеству В.
1=1² ∈ А
1=1³ ∈ В
Следовательно 1 ∈ А∩В.
4=2² ∈ А
4=(∛4)³ ∉ В
Следовательно 4 ∉ А∩В.
64=8² ∈ А
64=4³ ∈ В
Следовательно 64 ∈ А∩В.
б) Число принадлежит объединению множеств А и В, если оно принадлежит либо множеству А, либо множеству В.
16=4² ∈ А ⇒ 16∈А∪В
64=8² ∈ А ⇒ 64∈А∪В
27=3³ ∈ В ⇒ 27∈А∪В
№ 2
Рисунок в прикрепленном файле.
А - множество целых чисел, кратных 6.
В - множество целых чисел, кратных 12.
а) А∩В = В.
б) А∪В = А.


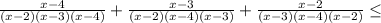
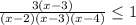
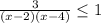
-5m^2+10mn-5n^2=-5(m-n)²
4ab-28b+8a-56=4b(a-y)+8(a-7)=(a-7)(4b+8)=4(a-7)(b+2)
A^4-81=(a²-9)(a²+9)=(a-3)(a+3)(a²+9)