ответ: (cos2x - sin^2x) / (2 * sin^2x - cos^2x) = - 1.
Объяснение:
1. Для того что бы упростить данное тригонометрическое выражение нам понадобится знание основных тригонометрических формул. В этом тригонометрическом выражении мы будем использовать вот эту формулу:
cos^2a + sin^2a = 1;
2. Подставим формулу cos^2a + sin^2a = 1, в тригонометрического выражения, получаем:
(cos2x - sin^2x) / (2 * sin^2x - cos^2x) = (cos^2a - sin^2a - sin^2a) / (2 * sin^2x - cos^2x) =
= ( - 2 * sin^2a + cos^2a) / (2 * sin^2x - cos^2x) =
= - (2 * sin^2x - cos^2x) / (2 * sin^2x - cos^2x) = - 1.
x = 0
Объяснение:
В основе решения таких неравенств лежит идея о знакопостоянствах функций. Дробь меньше нуля (т.е. отрицательна) только в том случае, если знак числителя не совпадает со знаком знаменателя. Чтобы найти промежутки, в которых эти знаки разнятся, допускают замену деления умножением, иными словами, решение неравенства
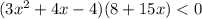
Проще всего такие неравенства решаются методом интервалов.
Для этого необходимо найти корни каждого из многочленов
1) 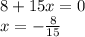
Стоит заметить, что мы приравниваем "бывший" знаменатель к нулю, лишь потому что нас интересуют интервалы знакопостоянства, а не только ради ОДЗ.
2) 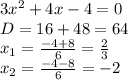
Вырисовываем две оси, отмечаем на них корни (необязательно соблюдать масштаб, главное - соблюсти порядок чисел: меньшие должны стоять левее)
+ - +
-------------|------------------------------|-------------->
-2 2/3
- +
--------------------------|-------------------------------->
-8/15
В тех интервалах, где знаки не совпадают, и будут нашим решением.
Это интервал (-∞;-2)∪(-8/15;2/3)
Так как от нас требуют найти наибольшее целое значение решения неравенства, то, очевидно, это будет 0.
б) 64x^6 - 1/27y^3z^3 = (4x^2)^3 - (1/3yz)^3 = (4x^2 - 1/3yz)(16x^4+4/3x^2yz + 1/9y^2z^2)
в) 7a^3 - 0,007 = 7(a^3 - 0,001) = 7(a^3 - 0,1^3) = 7(a - 0,1)(a^2+0,1a+0,01)
г) (b + 2)^3 - (b - 2)^3 = (b + 2 - b + 2)(b^2+4b+4 + b^2-4+b^2-4b+4)=
= 4(3b^2+ 4)
a) (4a + b)(16a^2 - 8ab - b^2) = 64a^3 + b^3 - неверно.
( 4a + b)( 16a^2 - 4ab + b^2) = 64a^3 + b^3 - верно.
б) (2a + 3b)(4a^2 - 6ab + 9b^2) = 8a^3 - 27b^3 - неверно.
(2a - 3b)(4a^2 + 6ab + 9b^2)= 8a^3 - 27b^3 - верно.