Найдите корни квадратного трехчлена: 1)х^2-10х+9 2)5х^2+12х+4

👇

Ответ:

Инна0606

09.03.2020

1) x²-10x+9 = 0
a =1; b = -10; c=9
D = b²-4ac
D = (-10)²- 4 ·9 = 100 - 36 = 64(√64=8)
x1 = -b+√D/2a ⇒ -(-10)+8/2 = 18/2 = 9.
x2 = -b-√D/2a ⇒ -(-10) -8/2 = 2/2 = 1.
2) 5x²+12x+4 = 0
a=5; b=12; c=4
D = b²-4ac
D = 12² - 4·5·4 = 144 - 80 = 64 (√64=8)
x1 = -b+√D/2a ⇒ -12+8/2·5 = -4/10 = -0,4.
x2 = -b-√D/2a ⇒ -12-8/2·5 = -20/10 = -2.

4,6(50 оценок)

Открыть все ответы

Ответ:

Boss2243

09.03.2020

Результаты исследования графика функции

Область определения функции. ОДЗ: Точки, в которых функция точно неопределена:x=2.00, x=-2.00.

Так как функция имеет 2 разрыва, то её область определения имеет 3 промежутка. От -00 до +00 на всех участках функция убывает.

На промежутках убывания производная функции отрицательна.

Точка пересечения графика функции с осью координат Y:График пересекает ось Y, когда x равняется 0: подставляем x=0 в 2*x/(x^2-4).
Результат: y=0. Точка: (0, 0)Точки пересечения графика функции с осью координат X:График функции пересекает ось X при y=0, значит нам надо решить уравнение:2*x/(x^2-4) = 0
Решаем это уравнение здесь и его корни будут точками пересечения с X: x=0. Точка: (0, 0)
Экстремумы функции:Для того, чтобы найти экстремумы, нужно решить уравнение y'=0 (производная равна нулю), и корни этого уравнения будут экстремумами данной функции:y'=-4*x^2/(x^2 - 4)^2 + 2/(x^2 - 4)=0
Решаем это уравнение и его корни будут экстремумами:Нет решения, значит, нет экстремумов.
Точки перегибов графика функции:Найдем точки перегибов для функции, для этого надо решить уравнение y''=0 - вторая производная равняется нулю, корни полученного уравнения будут точками перегибов указанного графика функции,
+ нужно подсчитать пределы y'' при аргументе, стремящемся к точкам неопределенности функции:y''=16*x^3/(x^2 - 4)^3 - 12*x/(x^2 - 4)^2=0lim y'' при x->+2.00
lim y'' при x->-2.00
(если эти пределы не равны, то точка x=2.00 - точка перегиба)
lim y'' при x->+-2.00
lim y'' при x->--2.00
(если эти пределы не равны, то точка x=-2.00 - точка перегиба)
Решаем это уравнение и его корни будут точками, где у графика перегибы:x=0. Точка: (0, 0)x=2.00. Точка: (2.00, ±oo)x=-2.00. Точка: (-2.00
Интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках изгибов:Вогнутая на промежутках: (-oo, 0] Выпуклая на промежутках: [0,oo)
Вертикальные асимптоты Есть: x=2.00 , x=-2.00 Горизонтальные асимптоты графика функции:Горизонтальную асимптоту найдем с предела данной функции при x->+oo и x->-oo. Соотвествующие пределы находим :lim 2*x/(x^2-4), x->+oo = 0, значит уравнение горизонтальной асимптоты справа: y=0 lim 2*x/(x^2-4), x->-oo = 0, значит уравнение горизонтальной асимптоты слева: y=0 Наклонные асимптоты графика функции: Наклонную асимптоту можно найти, подсчитав предел данной функции, деленной на x при x->+oo и x->-oo. Находим пределы :lim 2*x/(x^2-4)/x, x->+oo = 0, значит совпадает с горизонтальной асимптотой слеваlim 2*x/(x^2-4)/x, x->-oo = 0, значит совпадает с горизонтальной асимптотой справа
Четность и нечетность функции:Проверим функци четна или нечетна с соотношений f(x)=f(-x) и f(x)=-f(x). Итак, проверяем:2*x/(x^2-4) = -2*x/(x^2 - 4) - Нет 2*x/(x^2-4) = -(-2*x/(x^2 - 4)) - Да, значит, функция является нечётной/
Производная произведения константы на функцию есть произведение этой константы на производную данной функции.Применим правило производной частного:ddx(f(x)g(x))=1g2(x)(−f(x)ddxg(x)+g(x)ddxf(x))f(x)=x и g(x)=x²−4.Чтобы найти ddxf(x):В силу правила, применим: x получим 1Чтобы найти ddxg(x):дифференцируем x²−4 почленно:Производная постоянной −4 равна нулю.В силу правила, применим: x² получим 2xВ результате: 2xТеперь применим правило производной деления:(−x²−4)/x²−4)²Таким образом, в результате:( −2x²−8)/(x²−4)²Теперь упростим:−(2x²+8)/(x²−4)²

−(2x²+8)/(x2−4)²

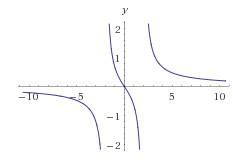
Найдите точки экстремума и определите промежутки возрастания-убывания функции y=2x/(x^2-4) поподробн

4,4(2 оценок)

Ответ:

Зояlove

09.03.2020

Y`=[2(x²-4)-2x*2x]/(x²-4)²=(2x²-8-4x²)/(x²-4)²=(-2x²-8)/(x²-4)²
y``=[-4x(x²-4)²-4x(x²-4)(-2x²-8)]/(x²-4)^4=-4x(x²-4)(x²-4-2x²-8)/(x²-4)^4=-4x(-x²-12)/(x²-4)^4=
=4x(x²+12)/(x²-4)³=0
x=0 критическая точка
x=-2 и x=2 точки разрыва

Отметим на числовой прямой две точки разрыва, критическую точку и определим знаки второй производной на полученных интервалах:

_ + _ +

-2 0 2

График функции y=4x/(x2-4)3 является вогнутым на (-2;0) U (2;∞) и выпуклым на (-∞;-2) U (0;2). В начале координат существует перегиб графика.

При переходе через точки x=-2 и x=2 вторая производная тоже меняет знак, но они не считаются точками перегиба, так как функция терпит в них бесконечные разрывы.

4,5(41 оценок)

Это интересно:

Кулинария-и-гостеприимство

20.03.2022

Секретный ингредиент коктейля «Арнольд Палмер» и его рецепт...

Финансы-и-бизнес

10.02.2022

Стартуем бизнес по схеме дропшиппинга: советы и рекомендации...

Компьютеры-и-электроника

01.06.2022

Как поднять свой боевой уровень в RuneScape: советы и рекомендации...

Стиль-и-уход-за-собой