Искомая функция 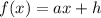 .
.
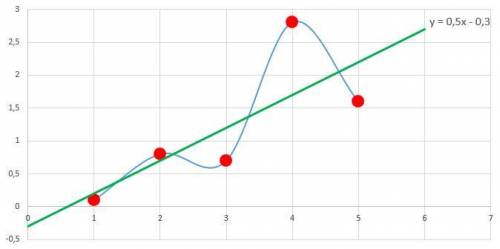
Найдем значения искомой функции в заданных точках х:
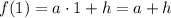
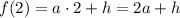
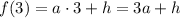
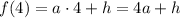
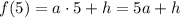
Кроме этого, для каждого из аргументов есть еще и экспериментальное значение, которое обозначим через функцию 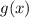 :
:
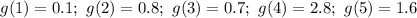
Составим функцию 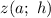 , которая будет суммировать квадраты разностей значений функций
, которая будет суммировать квадраты разностей значений функций 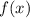 и
и 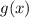 соответствующих аргументов:
соответствующих аргументов:
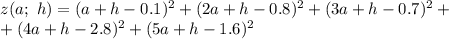
Исследуем эту функцию на экстремум.
Найдем частные производные:
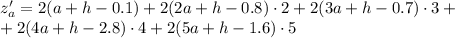
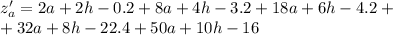
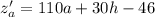
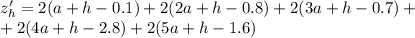
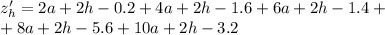
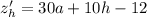
Необходимое условие экстремума: равенство нулю частных производных:
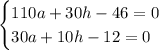
Домножим второе уравнение на (-3):
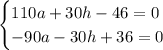
Складываем уравнения:
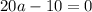
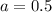
Подставим значение а во второе уравнение исходной системы:
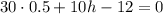
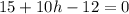
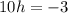

Точка (0.5; -0.3) - предполагаемая точка экстремума.
Найдем вторые частные производные функции:
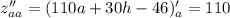
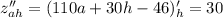
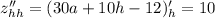
Рассмотрим выражение:

Так как 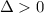 и
и 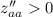 , то точка (0.5; -0.3) является точкой минимума.
, то точка (0.5; -0.3) является точкой минимума.
Значит, в точке (0.5; -0.3) функция 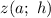 имеет минимум.
имеет минимум.
Тогда, значения 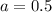 и
и  есть искомые коэффициенты функции
есть искомые коэффициенты функции 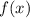 .
.
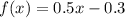
ответ: 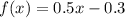
9 — 8x + 11 = 12
—8x = 12 — 20 = —8; x = 1;
2. (6x + 1) —(3 — 2x) = 14
6x + 1 — 3 + 2x = 14
6x + 2x = 14 + 2
8x = 16; x = 2;
3. 2x —(6x — 5) = 45
2x — 6x + 5 = 45
2x — 6x = 45 — 5
—4x = 40; x = —10;
4. 5x —(7x + 7) = 9
5x — 7x — 7 = 9
5x — 7x = 9 + 7
—2x = 16; x = —8;
5. 2x —(6x + 1) = 9
2x — 6x — 1 = 9
2x — 6x = 9 + 1
—4x = 10; x = —2,5;
6. 4x —(7x — 2) = 17
4x — 7x + 2 = 17
4x — 7x = 17 — 2
—3x = 15; x = —5;
7. 2x + 7 = 3x — 2 * (3x — 1)
2x + 7 = 3x — 6x + 2
2x — 3x + 6x = 2 — 7
5x = —5; x = —1;
8. 4 — 2 * (x + 3) = 4 * (x — 5)
4 — 2x — 6 = 4x — 20
—2x — 4x = —20 — 4 + 6
—6x = —18; x = 3;
9. 5x + 3 = 7x — 5 * (2x + 1)
5x + 3 = 7x — 10x — 5
5x — 7x + 10x = —5 — 3
8x = —8; x = —1;
10. 3y —(5 — y) = 11
3y — 5 + y = 11
3y + y = 11 + 5
4y = 16; y = 4.