1.400-m²=(20-m)(20+m)
2.4x²-25=(2x-5)(2x+5)
3.
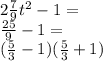
4.16a⁴-81=(4a²-9)(4a²+9)
5.(х+1)²-16=(х+1-4)(х-1-4)=(х-3)(х-5)
6.a²-12a+36=(a-6)²
7.16m²+24mn+9m²=25m²+24mn=m(25m+24n)
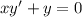
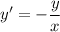 - уравнение с разделяющимися переменными
- уравнение с разделяющимися переменными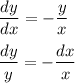
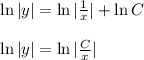
 - общее решение
- общее решение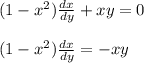

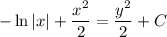 - общий интеграл
- общий интеграл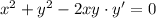

 , тогда
, тогда 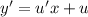



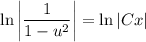
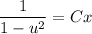
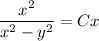 - общий интеграл
- общий интеграл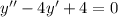
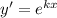 , тогда будем иметь характеристическое уравнение следующего вида:
, тогда будем иметь характеристическое уравнение следующего вида:
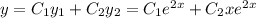 - общее решение
- общее решение
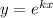 , тогда получаем
, тогда получаем
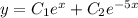

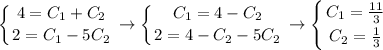
 - частное решение
- частное решение
обяснение в фоткe
посмотрите там