A) Верно, так как это теорема о задание арифметической прогрессии формулой an = kn + b, где k, b - некоторые числа.
Теорема. Любая арифметическая прогрессия (аn) может быть задана формулой an = kn + b, где k и b - некоторые числа; также имеет место обратное утверждение, если последовательность (аn) задана формулой an = kn + b, где k и b - некоторые числа, то эта последовательность является арифметической прогрессией.
Б) Не верно. Верна формула 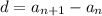
В) Неверно. Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних:
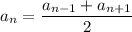
16xˇ2-4=4(4xˇ2-1)=4.(2x+1)(2x-1)
2x+6+xˇ2+3x=2(x+3)+x(x+3)=(x+3)(2+x)
2)2xˇ2+3x=0, x(2x+3)=0, x1=0,x2=-3/2
3)5abˇ2/abc=5b/c
4)(a+b)ˇ2-2ab+aˇ2-bˇ2=aˇ2+2ab+bˇ2-2ab+aˇ2-b2=2aˇ2=2.a.a=a.2a
5)xˇ3+2xˇ2-4x-8=0
xˇ2(x+2)-4(x+2)=0
(x+2)(xˇ2-4)=0
(x+2)(x+2)(x-2)=0
x1=-2,x2=-2,x3=2