Есть 12 вариантов выбора книг для покраски по количеству книг в каждом цвете (красный, зеленый, коричневый)
1 1 10
1 2 9
1 3 8
1 4 7
1 5 6
2 2 8
2 3 7
2 4 6
2 5 5
3 3 6
3 4 5
4 4 4
Им соответствуют количество вариантов выбора книг по их числу, например, первому, 12!/(10!*2!)*2!/(1!*1!)=66*2=132. Их надо посчитать.
И каждому набору соответствует число возможных перестановок по цветам. Если все числа в наборе разные, то 3!=6, если две одинаковые, до 3!/(2!*1!)=3, если все одинаковые (последний случай) , то 3!/(3!*0!)=1.
Затем количество вариантов выбора книг для каждого набора надо умножить на количество перестановок в наборе (то есть, для первого получится 132*3=396), и полученные числа сложить. Получится 519156.
В решении.
Объяснение:
1) Чтобы определить принадлежность точки графику, нужно известные значения х и у (координаты точки) подставить в уравнение. Если левая часть равна правой, то принадлежит, и наоборот.
а) у = 2х -3 А(-1; -5)
-5 = 2*(-1) - 3
-5 = -2 - 3
-5 = -5, принадлежит.
б) у = 2х -3 В(0; 3)
3 = 2*0 - 3
3 ≠ -3, не принадлежит.
в) у = 2х -3 С(-4; 7)
7 = 2*(-4) - 3
7 ≠ -11, не принадлежит.
г) у = 2х -3 Д(2,5; 2)
2 = 2*2,5 - 3
2 = 5 - 3
2 = 2, принадлежит.
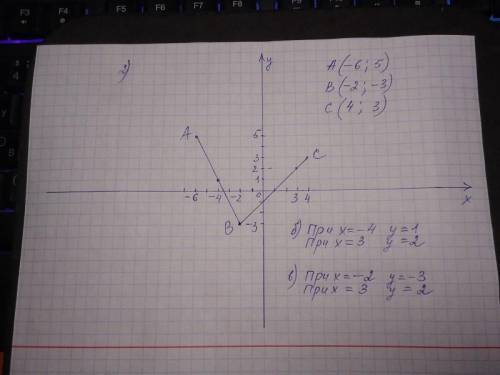
2) На фото.
3)
а) Область определения - это проекция графика на ось Ох, все значения х, при которых функция существует. Согласно рисунка, функция существует при значениях х от -2 до 7, значит, область определения D(f) = [-2; 7].
Кружки на концах графика закрашены, это значит, что значения х= -2 и х=7 входят в область определения функции, скобки квадратные.
б) Область значений функции - это проекция графика на ось Оу, означает, в каком интервале существуют значения функции. Согласно рисунка, эти значения от у= -2 до у= 4,8, значит, область значений
Е(f) = [-2; 4,8], скобки также квадратные.
в) f(3) - запись говорит о том, что нужно найти значение у при х=3. Согласно рисунка, при х=3 у=3.
г) f(x) = 2, запись говорит о том, что нужно найти значение х при у=2. Согласно рисунка, при х=2 у=2.
д) Точка одна, координаты (6,5; 0).
е) Определить значения х, при которых у < 0, это график ниже оси Ох.
у < 0 при х∈(6,5; 7), то есть при х от 6,5 до 7.
ж) Определить значения х, при которых у > 0, это график выше оси Ох.
у > 0 при х∈(-2; 6,5), то есть при х от -2 до 6,5.
4^(-12) /4^(-8+(-2)) =4^(-12) / 4^(-10) =4^(-12-(-10))=4^(-2) =1/4² =1/16
x^(-1) =1/x^1
при делении степени вычитаются, а при умножении степени складываются