Алгебра: Sin2x умножить на корень из sinx = 0

Sin2x умножить на корень из sinx = 0

👇

Увидеть ответ

Ответ:

ассасин32

13.02.2022

sin2x=0 ,2x=П .n , n-целое число, Х=П/2.n , n-целое число

2) sin x=0, x =П .n , n-целое чиспо

При четных значениях n первое множество вкючает второе множество, оветом будет первое множество.

4,8(62 оценок)

Ответ:

ВалентинЛаднов

13.02.2022

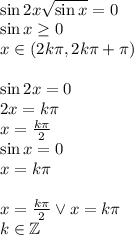
$\\\sin 2x\sqrt{\sin x}=0\\ \sin x \geq0\\ x\in(2k\pi,2k\pi+\pi)\\\\ \sin2x=0\\ 2x=k\pi\\ x=\frac{k\pi}{2}\\ \sin x=0\\ x=k\pi\\\\ x=\frac{k\pi}2 \vee x=k\pi\\ k\in\mathbb{Z}$

4,6(4 оценок)

Открыть все ответы

Ответ:

мядель

13.02.2022

1. Сложить два известных угла, результат вычесть из 180 градусов.

2. Вычесть известный угол из 90 градусов; сложить известный угол с 90, результат вычесть из 180 градусов.

3. 82

4. 98

5. Отрезок BH образует со стороной АС угол в 90 градусов.

6. Точка M разделит отрезок АС пополам.

7. Отрезок BE разделит угол В пополам.

8. Углы при основании равны; биссектриса, проведенная к основанию, является медианой и высотой

9. Касательная, проведенная к окружности, перпендикулярна радиусу, проведенному к точке касания; из любой точки, лежащей вне окружности, можно провести ровно две касательные к окружности; отрезок, соединяющий точку, лежащую вне окружности, с центром окружности, является биссектрисой угла между касательными, проведенными из этой точки к окружности; отрезки касательных (к одной окружности!), проведенных из одной точки, равны.

10. Медианы делятся в отношении 2:1 считая от вершин треугольника.

4,7(23 оценок)

Ответ:

браинли56

13.02.2022

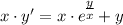
$x\cdot y'=x \cdot e^\big{ \frac{y}{x} }+y$
Убедимся, что данное дифференциальное уравнение является однородным.

То есть, воспользуемся условием однородности
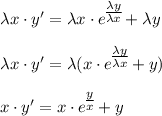
$\lambda x\cdot y'=\lambda x \cdot e^\big{ \frac{\lambda y}{\lambda x} }+\lambda y\\ \\ \lambda x\cdot y'=\lambda(x \cdot e^\big{ \frac{\lambda y}{\lambda x} }+y)\\ \\ x\cdot y'=x \cdot e^\big{ \frac{y}{x} }+y$
Итак, данное дифференциальное уравнение является однородным.

Однородное дифференциальное уравнение сводится к уравнению с разделяющимися переменными относительно новой неизвестной функции u=u(x)

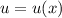с замены:

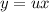, тогда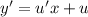

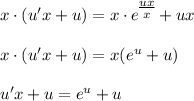
$x\cdot (u'x+u)=x\cdot e^\big{ \frac{ux}{x} }+ux\\ \\ x\cdot (u'x+u)=x(e^u+u)\\ \\ u'x+u=e^u+u$

u'x=e^u

По определению дифференциала, получаем
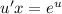
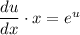$\dfrac{du}{dx} \cdot x=e^u$ - уравнение с разделяющимися переменными.
Разделим переменные.
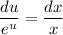$\dfrac{du}{e^u} = \dfrac{dx}{x}$ - уравнение с разделёнными переменными.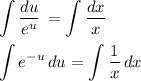

Проинтегрируем обе части уравнения
$\displaystyle \int\limits { \frac{du}{e^u} } \,=\int\limits { \frac{dx}{x} } \\ \\ \int\limits {e^{-u}} \, du=\int\limits { \frac{1}{x} } \, dx$
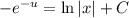$-e^{-u}=\ln |x|+C$ - общий интеграл новой функции.

Таким образом, определив функцию

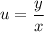
из решения уравнения с разделяющимися переменными, чтобы записать решение исходного однородного уравнения, остаётся выполнить обратную замену: $u= \dfrac{y}{x}$

То есть,

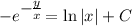$-e^\big{-\frac{y}{x} }=\ln |x|+C$ - общий интеграл исходного уравнения.
Остаётся определить значение произвольной постоянной

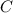. Подставим в общий интеграл начальное условие: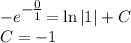
$-e^\big{- \frac{0}{1} }=\ln |1|+C\\ C=-1$

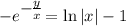$-e^\big{-\frac{y}{x} }=\ln |x|-1$ - частный интеграл, также является решением данного дифференциального уравнения.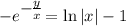

ответ: $-e^\big{-\frac{y}{x} }=\ln |x|-1$

4,8(8 оценок)

Это интересно:

Кулинария-и-гостеприимство

06.06.2022

Как приготовить конфеты из сахара...

Компьютеры-и-электроника

06.03.2022

Как сбросить пароль учетной записи на Instagram: мастер-класс с шаг за шагом инструкцией...

Компьютеры-и-электроника

11.08.2021

Как настроить iPod Touch: подробное руководство...

Кулинария-и-гостеприимство