172.
1) 5^(x+y)=125, (1)
3^((x-y)²-1)=1; (2)
5^(x+y)=5³, (1)
3^((x-y)²-1)=3^0; (2)
x+y=3, (1)
(x-y-1)(x-y+1)=0; (2)
y=3-x, (1)
(x-3+x-1)(x-3+x+1)=0; (2)
(2x-4)(2x-2)=0;
2x-4=0;
2x=4;
x1=2
или
2x-2=0;
2x=2;
x2=1.
y1=3-2=1;
y2=3-1=2.
ответ: (2;1), (1;2).
2) 3^x+3^y=12, (1)
6^(x+y)=216; (2)
6^(x+y)=6³;
x+y=3;
y=3-x;
3^x+3^(3-x)=12; (1)
3^(2x)-12*3^x+27=0;
3^x=t;
t²-12t+27=0;
D=144-108=36;
t1=(12-6)/2=3;
t2=(12+6)/2=9;
3^x=3;
x1=1;
3^x=9;
x2=2;
y1=3-1=2;
y2=3-2=1.
ответ: (1;2), (2;1).
3) 4^(x+y)=128, (1)
5^(3x-2y-3)=1; (2)
2^(2(x+y))=2^7, (1)
5^(3x-2y-3)=5^0; (2)
2x+2y=7, (1)
3x-2y-3=0; (2)
2y=7-2x, (1)
3x-7+2x-3=0; (2)
6x=10;
x=10/6=5/3;
y=(7-2x)/2=(7-10/3)/2=11/6.
ответ: (5/3;11/6).
4) 3^(2x-y)=1/81, (1)
3^(x-y+2)=27; (2)
3^(2x-y)=3^(-4), (1)
3^(x-y+2)=3³; (2)
2x-y=-3, (1)
x-y+2=3; (2)
x-y=1;
y=x-1;
2x-x+1=-3; (1)
x=-4;
y=-4-1=-5.
ответ: (-4;-5).
173.
1) 4^(x+y)=16, (1)
4^(x+2y-1)=1; (2)
4^(x+y)=4², (1)
4^(x+2y-1)=4^0; (2)
x+y=2, (1)
x+2y-1=0; (2)
y=2-x; (1)
x+2(2-x)-1=0; (2)
x+4-2x-1=0;
-x=-3;
x=3;
y=2-3=-1.
ответ: (3;-1).
2) 6^(2x-y)=√6, (1)
2^(y-2x)=1/√2; (2)
6^(2x-y)=6^(1/2); (1)
2^(y-2x)=2^(-1/2); (2)
2x-y=1/2, (1)
+
y-2x=-1/2; (2)
0=0
ответ: нет решений.
3) 5^(2x+y)=125, (1)
7^(3x-2y)=7; (2)
5^(2x+y)=5³, (1)
7^(3x-2y)=7^1; (2)
2x+y=3, (1)
3x-2y=1; (2)
y=3-2x; (1)
3x-2(3-2x)=1;
3x-6+4x=1;
7x=7;
x=1;
y=3-2*1=1.
ответ: (1;1).
4) 3^(4x-3y)=27√3, (1)
2^(4y+x)=1/(2√2); (2)
3^(4x-3y)=3^(7/2), (1)
2^(4y+x)= 2^(-3/2); (2)
4x-3y=7/2, (1)
4y+x=-3/2; (2)
x=-3/2-4y,
4(-3/2-4y)-3y=7/2; (1)
-6-16y-3y=7/2;
-19y=19/2;
y=-1/2;
x=-3/2-4(-1/2)=-3/2+2=1/2.
ответ: (1/2;-1/2).
 ;
;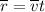 ;
;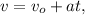 либо в векторном виде:
либо в векторном виде: 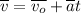 ;
;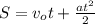 либо в векторном виде:
либо в векторном виде: 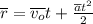 ;
;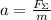 либо в векторном виде:
либо в векторном виде: 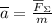 ;
; ;
;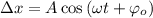 ;
;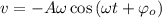 ;
; ;
;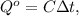 где
где 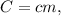 либо в удельном виде:
либо в удельном виде:  ;
;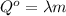 ;
;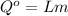 ;
; ;
; ;
;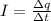 ;
;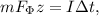 где
где  ;
;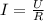 ;
;
 ;
; ;
; ;
;
приводим к нулям функции то есть приравниваем всё это выражение к нулю
получаем уравнение которое решается через дискриминант, и дискриминант равен 0, следовательно х=0,2
рисуем координатную прямую х
отмечаем точку 0,2 и закрашиваем так как знак не строгий
рисуем параболу ветвями вверх, так как коэффициент при х^2=25 и он больше нуля
далее отмечаем интервал и получаем промежуток
(-∞;0,2|^|0,2;+∞)