Случайная величина Х - количество попаданий в кольцо. Случайная величина распределена по биномиальному закону. Вероятность успеха в одном испытании p = 0.1, тогда q = 1 - p = 0.9
1) Вероятность того, что баскетболист не попадает в кольцо ниразу
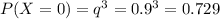
2) Вероятность того, что баскетболист попадет один раз
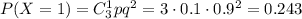
3) Вероятность того, что баскетболист попадет два раза
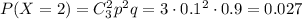
4) Вероятность того, что баскетболист попадет три раза
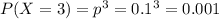
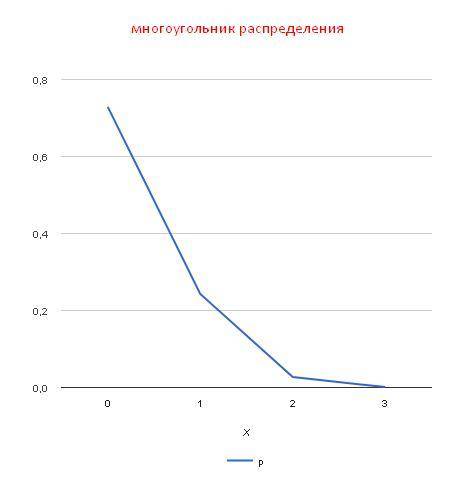
Закон распределения случайной величины X:
Xi 0 1 2 3
Pi 0.729 0.243 0.027 0.001
Математическое ожидание случайной величины X:
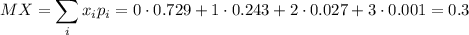
Иначе мат. ожидание можно подсчитать, если Х - распределена по биномиальному закону то 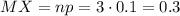
Дисперсия случайной величины X:
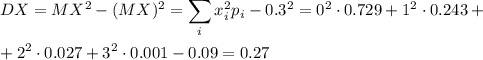
Иначе: 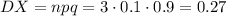
Среднее квадратическое отклонение:
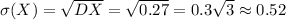
Нам необходимо найти сумму первых семи членов арифметической прогрессии. Для этого нам нужно воспользоваться формулой:
Sn=((2a1+(n-1)d)/2)*n
где a1-первый член арифметической прогрессии,
n-количество членов прогрессии,
d-разность данной арифметической прогрессии.
Нам необходимо найти a1. Но, из условия задачи, нам дано только a12=-2, d=1. Мы знаем, что n-ый член прогрессии можно найти из формулы:
an=a1+d(n-1)
Выразим из данной формулы a1:
a1=an-d(n-1)
a12=-2, d=1, n=12
a1=an-d(n-1)=a12-d(12-1)=-2-1(12-1)=-2-11=-13
Тогда S7=?
a1=-13, d=1, n=7
S7=((2a1+(n-1)d)/2)*n=((2*(-13)+(7-1)*1)/2)*7=((-26+6)/2)*7=(-20/2)*7=-10*7=-70
Объяснение:
15 + 3а = - 6 - 4а
3а + 4а = - 6 - 15
7а = - 21
а = - 3
ответ при а = - 3