Все в объяснениях.
Объяснение:
1. Постройте график функции y=f(x).
Гипербола, полученная сдвигом графика у=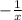
на 1 вверх по оу. у(-2)=0,5 ;у(-1)=1 ;у(-2)=0,5 ;у(2)=-0,5 ;у(1)=-1 ;у(2)=-0,5
2. f '(x)= (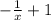 
) ' =
.
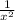3. Уравнения касательной y =к (x −x₀)+f (x₀) .
Прямая y=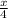
, к=1\4.
Найдем точку касания
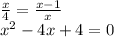
(x-2)²=0 , x=2.
f (2)=-1\2+1=0,5
y =0,25* (x −2)+0,5
у=0,25х
Вторая касательная пройдет через х=-2
f (-2)=1\2+1=1,5
y =0,25* (x −2)+1,5
у=0,25х+1
4. Наименьшее значение функции у'=(x−f(x) ) '=(х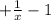
)' =
=1 -=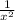
.
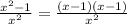у'=0 ,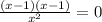 
,х=1 , х=-1.
На промежутке [1/2;∞) лежит только х=1
у'______[1\2] - - - - -(1)+ + + + +
y ↓ ↑
x=1 точка минимума.
Наименьшее значение может быть при х=1\2 или х=1:
у(1\2) =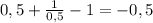
.
у(1)= 1+1-1=1.
Наименьшее значение функции х-f(x) равно -0,5
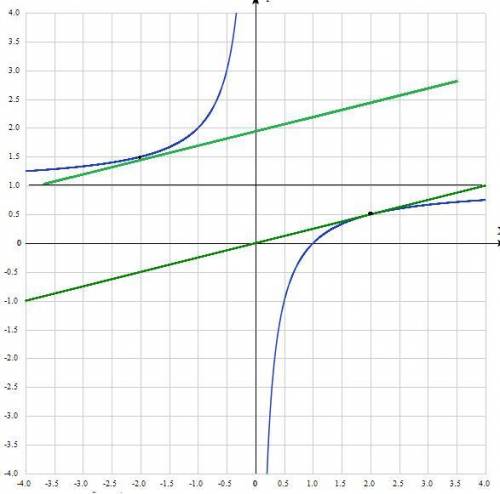
решение на фотографии
Объяснение:
м. Крамера: находим 4 определителя.
1: это основная матрица
2: вместо первого столбика пишем числа, не относящиеся к переменным, - это -6, -5 и -2.
3: числа вместо 2 столбика
4: числа вместо 3 столбика
Далее по формулам также ищем значения самих переменных.
м Гаусса: меняются только строки, рядом с которыми написаны действия.
Допустим, 1я матрица, рядом с первой строкой I-III, значит из первой строки вычитаем числа третьей строки. В следующей матрице 1я строка полностью изменила. Где-то мы можем дорожать строки на числа и потом их прибавлять или отнимать, но мы их не меняем в следующей матрице. Должны получится единичная матрица, а числа за чертой, справа, это значения переменных.
sin3x-sin(π/2-2x)=0
2sin(x/2-π/4)cos(5x/2+π/4)=0
sin(x/2-π/4)=0⇒x/2-π/4=πn⇒x/2=π/4+πn⇒x=⇒/2+2⇒n,n∈z
cos(5x/2+π/4)=π/2+πk⇒5x/2=π/4+πk⇒x=π/10+2πk/5,k∈z
2
2sinx-3cosx-3=0
4sin(x/2)cos(x/2)-3cos²(x/2)+3sin²(x/2)-3sin²(x/2)-3cos²(x/2)=0
4sin(x/2)cos(x/2)-6cos²(x/2)=0
2cos(x/2)*(2sin(x/2)-3cos(x/2))=0
cos(x/2)=0⇒x/2=π/2+πn⇒x=π+2πn,n∈z
2sin(x/2)-3cos(x/2)=0/cos(x/2)
2tg(x/2)-3=0⇒tg(x/2)=1,5⇒x/2=arctg1,5+πk⇒x=2arctg1,5+2πk,k∈z