1) ac2-ad+c3-cd-bc2+bd= = (ac2 – ad) + (c3 –
bc2) + (bd – cd) = a·(c2 – d) + c2·(c – b) + d·(b – c) = a·(c2 – d) +
c2·(c – b) – d·(c – b) = a·(c2 – d) + c2·(c – b) – d·(c – b) = a·(c2 –
d) + (c – b)·(c2 – d) = (c2 – d)·(a + c – b)
2) mx2+my2-nx2-ny2+n-m= x2 ( m - n ) + y2 ( m - n ) - ( m - n ) = ( m-n ) (x2 + y2 - 1 )
3) am2+cm2-an+an2-cn+cn2= m2 (a + c ) + n2 ( a + c ) - n ( a + c ) = ( a+ c) ( m2 + n2 - n)
4) xy2-ny2-mx+mn+m2x-m2n= y2 ( x - n ) + m2 ( x - n) - m ( x - n ) = ( x-n) ( y2 + m2 - m )
5) a2b+a+ab2+b+2ab+2=ab ( a + b + 2 ) + ( a+ b+ 2 ) = 2 ( a+ b + 2 )
6) x2-xy+x-xy2+y3-y2= x ( x – y + 1) – y 2 ( x – y + 1)=( x – y + 1)( x – y 2 ).
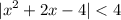
раскроем модуль:
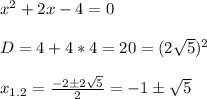
_+___ -1 -√5 ___-___ -1+√5__+__
x²+2x-4 -x²-2x+4 x²+2x-4
1) теперь рассмотрим решение неравенства на промежутках
(-∞; -1-√5] ∪ [-1+√5; +∞)
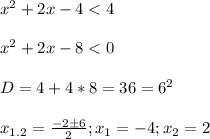
_\\\\\\ -4 _\\\\\ -1-√5_____ -1+√5_\\\\\\_ 2__\\\\\__
////////////////////////////////////////////////
пересечением решений будут промежутки
(-4; -1-√5] ∪ [-1+√5;2)
2) теперь рассмотрим решение неравенства на промежутках
(-1-√5;-1+√5)
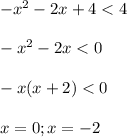
_____ -1-√5_ \\\\\\_ -2_\\\\\\_ 0_\\\\\_-1+√5_____
//////////////////////////// /////////////////////
пересечением решений будут промежутки (-1-√5;-2) ∪ (0; -1+√5)
И Тогда общим ответом будет
(-4; -2) ∪ (0;2)