(1; 10), (11; -10), (-1; -10) и (-11; 10).
Объяснение:
Число 11 - простое и может быть представлено в виде произведения двух целых чисел только таким образом: а) 1 × 11 = 11 или б) -1 × (-11) = 11. Рассмотрим произведения по отдельности.
а) Любой из множителей может быть равным 1 и любой из множителей может быть равен 11. Поэтому рассмотрим два случая:
1) если х = 1, то х + у = 11; 1 + у = 11; у = 10. Пара чисел (1; 10) - первое решение.
2) если х = 11, то х + у = 1; 11 + у = 1; у = -10. Пара чисел (11; -10) - второе решение.
б) любой из множителей может быть равным -1 или -11. Поэтому вновь рассматриваем два случая:
1) если х = -1, то х + у = -11; -1 + у = -11; у = -10. Пара чисел (-1; -10) - третье решение.
2) если х = -11, то х + у = -1; -11 + у = -1; у = 10. Пара чисел (-11; 10) - четвертое решение.
Итого в целых числах данное уравнение имеет четыре решения: (1; 10), (11; -10), (-1; -10) и (-11; 10).
ответ: 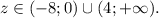
Объяснение:
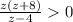
На каждом из интервалов (-∞; -8); (-8; 0); (0;4); (4; +∞) левая часть неравенства принимает значения только одного знака.
1. (-∞; -8) : z < 0; z+8 < 0; z-4 < 0; значит левая часть неравенства меньше 0;
2.(-8; 0): z < 0; z+8 > 0; z-4 < 0; значит левая часть неравенства больше 0;
3.(0; 4): z > 0; z+8 > 0; z-4 < 0; значит левая часть неравенства меньше 0;
4.(4; +∞): z > 0; z+8 > 0; z-4 > 0; значит левая часть неравенства больше 0;
Подходят только (-8; 0) и (4; +∞).
2tg^2 x + 1 + 3tgx - 3 = 0
2tg^2 x + 3tgx - 2 = 0
пусть tgx=a, где a - любое число; тогда уравнение принимает вид
2a^2 + 3a - 2 = 0
D= 3^ - 4*(-2) * 2 = 9 + 16 = 25 √25 = 5
a1 = (-3 + 5) / 2*2 = 2/4 = 1/2 = 0.5;
a2 = (-3 - 5) / 4 = -8 / 4 = -2;
tgx = -2 tgx = 0.5
x= -arctg2 + πk, k∈Z; x = arctg0.5 + πm, m∈Z;
Думаю, так.