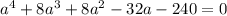
произведём замену переменных
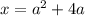
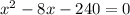
Cчитаем дискриминант:
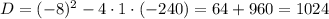
Дискриминант положительный
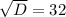
Уравнение имеет два различных корня:
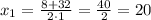
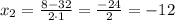
исходное уравнение сводится к уравнению
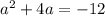
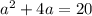
================================================
Случай 1
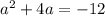
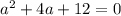
Cчитаем дискриминант:
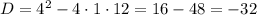
Дискриминант отрицательный, следовательно уравнение не имеет действительных решений
=================================================
Случай 2
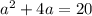
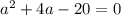
Cчитаем дискриминант:
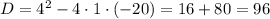
Дискриминант положительный
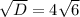
Уравнение имеет два различных корня:
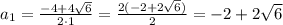
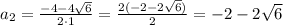
ответ: 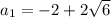 ;
; 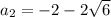
Объяснение:
udv + vdu или udv = d(uv) - vdu.
Для выражения d(uv) первообразной, очевидно, будет uv, поэтому имеет место формула:
∫ udv = uv - ∫ vdu (8.4.)
Эта формула выражает правило интегрирования по частям. Оно приводит интегрирование выражения udv=uv'dx к интегрированию выражения vdu=vu'dx.
Пусть, например, требуется найти ∫xcosx dx. Положим u = x, dv = cosxdx, так что du=dx, v=sinx. Тогда
∫xcosxdx = ∫x d(sin x) = x sin x - ∫sin x dx = x sin x + cosx + C.
Правило интегрирования по частям имеет более ограниченную область применения, чем замена переменной. Но
(- 2,3 - 3,91 / (- 2,3)) / (- 0,01) * (-0,7) = - 42.
1) 3,91 / (- 2,3) = - 1,7;
2) - 2,3 - (- 1,7) = - 2,3 + 1,7 = - 0,6;
3) - 0,6 / (- 0,01) = 60;
4) 60 * (- 0,7) = - 42.
ответ: - 42.
Объяснение:
Для того, чтобы решить задания, нужно соблюдать правильный порядок выполнения арифметических действий: 1) сначала сделаем действие в скобках; 2) потом - деление и умножение; 3) последним - добавление и вычитание. Когда перед скобками стоит минус, то знаки в скобках меняются на противоположные. Если допустить ошибку, результат будет ошибочным.
файл