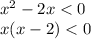
Решаем с метода интервалов: 1). для этого все выражения с х приравниваем к нулю и решаем полученные уравнения (х=0, х= 2);
2). определяем точки, которые соответствуют найденным нулям и отмечаем их выколотыми точками (т.к. неравенство строгое) на оси координат;
3). определяем знаки выражения f(x)
из левой части решаемого неравенства на каждом промежутке и проставляем их на графике;
4). наносим штриховку над нужными участками графика, руководствуясь следующим правилом: в случае, если неравенство имеет знак <, то изображается, штрихуются «минусовые» промежутки.
5). Заштихованный промежуток и будет являться ответом.
ответ: (0;2).
каждое подмодульное выражение = 0 при х = 0; 7; 2.
Учтём, что |x| ,= x при х ≥ 0
|x| = -x при х < 0
Наша числовая прямая делится нашими числами на 4 промежутка. Получим 4 уравнения.
1) (-∞ ; 0) (*)
-х +7 - х -2(х-2) = 4
-х +7 -2х +4 = 4
-3х = -7
х = 7/3 ( не входит в (*))
2) (0;2) ( **)
х -7 +х -2(х-2) = 4
х -7 +х -2х +4 = 4
-х = 7
х = -7 ( не входит в (**))
3) (2;7) (***)
х +7 - х +2(х -2) = 4
х +7 - х +2х -4 = 4
2х = 15
х = 15/2
х = 7,5 ( не входит в (***))
4) (7;+∞) ( )
х -7 +х + 2(х -2) = 4
х -7 +х +2х -4 = 4
4х = 15
х = 15/4 = 3,75 ( не входит в ())
ответ: нет решений.