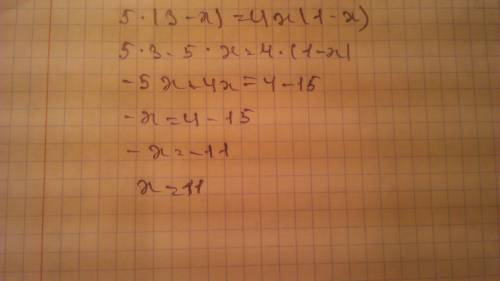
1. Рабочих станет 20·1,2=24.
Имеем обратную пропорциональную зависимость. Учитывая это, составляем пропорцию:
30-24
х-20
х=30·20/24=25
30-25=5 (дней)
ответ. на 5 дней быстрее
2. Пусть производительность рабочего была равна 1, а стала равна 1,2 .
Время сначала обозначим 100 %, а после повышения производительности - х. Составим пропорцию, учитывая, что пропорциональность обратная:
1-х
1,2-100
х=100/1,2=83 1/3 %
Находим, на сколько уменьшилось время.
100 % - 83 1/3 % =16 2/3 %
ответ. 16 2/3 %
3. Осталась 1/3 воды, температура которой 100°, и долили 2/3 воды, температура которой 16°. Имеем:
(1·100+2·16)/3=44°
ответ. 44°
Скорректирую решение первой задачи.
Находим производную данной ф-ии:
Y' = -4sin2x + cosx >=0 (ищем промежутки возрастания(убывания) и крит. точки)
cosx(1 - 8sinx) >=0
Отмечаем на окружности четыре критические точки:
arcsin(1/8), П - arcsin(1/8), П/2, -П/2.
Анализируя получившиеся 4 интервала приходим к выводу, что в точках:
arcsin(1/8), П - arcsin(1/8) функция достигает своего максимума, а в точках:
П/2, -П/2 - минимума.
Найдем эти значения: (sinx = 1/8, cos2x = 1-2sin^2(x) = 31/32)
Уmax = 62/32 - 1/8 - 1 = 26/32 = 13/16
Ymin = -2 -1 -1 = -4
Получим следующую область значений: [ -4; 13/16]