Итак, нам нужно найти расстояние между пунктами А и В. Давайте его сразу и обозначим за 
(километров).
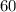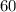км/ч. То есть, нам известно расстояние, которое проехал автомобиль (оно равно ) и его скорость ( км/ч). Вопрос: что мы можем найти? Конечно же, время. Оно равно пройденному расстоянию, деленному на скорость: 
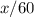(часов).А давайте теперь попробуем определить время, затраченное автобусом. Расстояние будет таким же - ровно километров, но двигаться наш транспорт будет помедленнее - со скоростью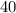 
км/ч. При этом находить время мы будем также: 
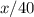(часов).Нам известно (ну или почти известно...) время, затраченное обоими видами транспорта на путь. Только что теперь с этим делать?
В условии сказано: "автомобиль приехал в пункт В на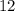 
минут раньше автобуса". Задумаемся: автомобиль ехал 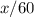часов, а автобус - 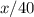часов. И, по условию, разность этих двух чисел равна 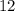минут. Это и есть ключевой момент задачи!
(!) Только не стоит торопиться! 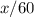и 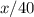мы измеряли в часах, и было бы странно в виде разности получить минуты. Так что не будем лишний раз испытывать умение решать уравнения и переведем 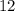минут в часы. Наверное, в часе 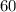минут (пусть это в задаче и не оговорено), поэтому 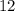минут - это 
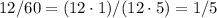часа.
Значит, имеем уравнение: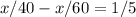 
(вычитаем именно из 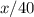, так как это - время автобуса, и, разумно предположить, что оно больше времени автомобиля).
Ничего иного не остается, кроме как решить полученное уравнение:
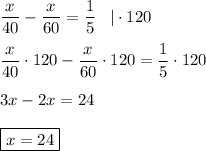
Это и есть ответ задачи!
Для уверенности можем сделать проверку:
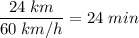(время автомобиля);
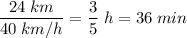(время автобуса);
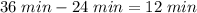(разность).Все сходится, задача решена!
Если останутся вопросы по такому виду задач, задавайте!
ответ:24 километра.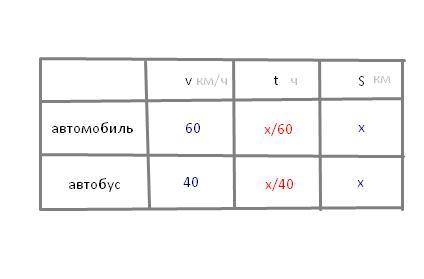
Функция f(x)=4x³+8x²+9;
а) найти промежутки возврастания(убывания) ;
б ) найти критические точки .
f '(x) = (4x³+8x²+9) ' =(4x³) ' +(8x²) '+( 9) '=4(x³) ' +8(x²) '+0 =4*3x² +8*2x =
12x(x+4/3) ; D(f '(x) ) : x ∈ R
Функция убывает (↓) ,если f '(x) ≤ 0 ( возрастает, если f '(x) ≥ 0 )
12(x+4/3)x ≤ 0 ⇒ x∈ [ - 4/3 ; 0 ]
[ - 4/3 ] [0]
f ' (x) "+" " -" " +"
f(x) ↑ ↓ ↑
Функция возрастает промежутках ( -∞ ; -4/3] и [ 0 ; ∞) ;
убывает в промежутке [ - 4/3 ; 0]
- - - - - - -
б) Критические точки : f '(x) = 0 ⇔ (x+4/3)x =0 ⇒ x = - 4/3 и x=0 , притом эти критические точки являются точками экстремумов .
x = - 4/3 точка максимума ; x=0 _точка минимума.
3у=81-6х
у=(81-6х)/3=3(27-2х)\3
у=27-2х