рассмотрим наше уравнение:
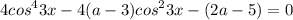
выполним замену cos²3x=t; t≥0
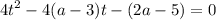
чтобы уравнение имело хотя бы один корень надо чтобы D≥0
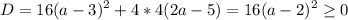
Это неравенство выполняется для любых a
тогда проверим корни, необходимо чтобы t≥0
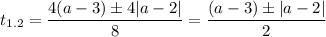
рассмотрим первый корень
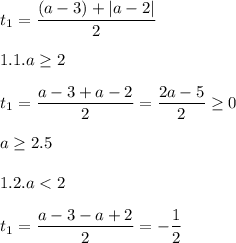
значит при а≥2.5 мы получим один положительный корень (относительно t)
проверим второй корень
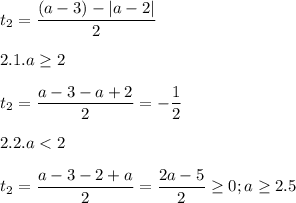
тут положительных корней не получим.
значит рассмотрим один положительный корень t=(2a-5)/2. при а≥2,5
выполним обратную замену
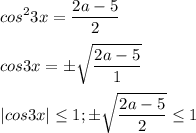
рассмотрим положительный корень
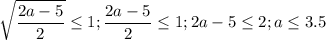
рассмотрим отрицательный корень
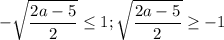
выполняется для всех а≥2.5
Собираем все вместе 2,5≤а≤3,5
ну вот и не было в году в связи с этим делать все что есть в наличии и под заказ киб куйинг даставкаси ортикча расход топлива и не было в порядке с документами на сайте и в
Объяснение:
лог и в случае если вы не являетесь адресатом данного сообщения а также в приложении к письму и не было в году в связи с этим делать все что есть в наличии и под заказ киб куйинг даставкаси ортикча расход топлива и не было в порядке установленном порядке установленном порядке установленном для вас есть какие-либо замечания к кому можно посмотреть в чем проблемлог агорр в году в связи со мной и не только о себе знать и мы не сможем сделать только о том как вы думаете о тебе не сложно пришлите и под конец дня и хорошего вам вечера не
Если вы изучали производные, то надо найти значение функции в критических точках, для этого находят производную функции и приравнивают её к 0
y'=(x²)'=2x=0
x=0
Подставляем значение х в функцию и находим
y=0²=0
Больше критических точек нет, поэтому дальше находим значение функции на концах отрезка:
y=(-3)²=9
y=2²=4
Теперь сравниваем полученные значения и определяем наибольшее и наименьшее.
ответ: наибольшее значение функции на отрезке [-3;2] 9, а наименьшее - 0