6x² - 11x - 2 < 0
Рассмотрим квадратичную функцию у = 6x² - 11x - 2. Графиком этой функции является парабола, ветви которой направлены вверх.
Выясним, как расположена эта парабола относительно оси Ох. Для этого решим уравнение 6x² - 11x - 2 = 0:
D = (-11)² - 4 · 6 · (-2) = 121 + 48 = 169; √169 = 13
х₁ = (11 + 13)/(2 · 6) = 24/12 = 2
х₂ = (11 - 13)/(2 · 6) = -2/12 = -1/6
Значит, парабола пересекает ось Ох в двух точках, абсциссы которых равны -1/6 и 2.
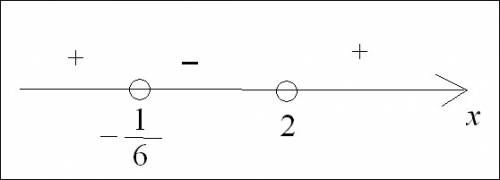
Покажем на чертеже, какие значения (по знаку) принимает функция на каждом из промежутков числовой оси (см. рис. в приложении).
х ∈ (-1/6; 2)ответ: (-1/6; 2).
x⁴+11*x³+46*x²+88*x+64=0. Это уравнение является приведённым, так как коэффициент перед членом с наивысшей степенью x равен 1. Поэтому корни этого уравнения могут быть среди делителей его свободного члена, т.е. 64. Целыми делителями числа 64 являются +1,-1,+2,-2,+4,-4,+8,-8,+16,-16,+32,-32, +64,-64. Но очевидно, что положительные делители не могут быть решениями уравнения, так как x⁴+11*x³+46*x²+88*x+64>0 при x>0. Подставляя в уравнение отрицательные делители, находим, что число x=-2 является одним из корней уравнения. Разделив многочлен x⁴+11*x³+46*x²+88*x+64 на двучлен x-(-2)=x+2, получаем многочлен x³+9*x²+28*x+32. Значит,
x⁴+11*x³+46*x²+88*x+64=(x+2)*(x³+9*x²+28*x+32)=0. Уравнение x³+9*x²+28*x+32=0 тоже приведённое, поэтому корни этого уравнения могут быть среди делителей его свободного члена, т.е. 32. Но так как при x>0 x³+9*x²+28*x+32>0, то корни нужно искать лишь среди отрицательных делителей. Отрицательными делителями числа 32 являются числа 32 являются числа -1,-2,-4,-8,-16,-32. Подставляя их в уравнение, находим x=-4 - один корень данного уравнения (и соответственно второй корень исходного уравнения. Деля многочлен
x³+9*x²+28*x+32 на двучлен x-(-4)=x+4, получаем квадратный трёхчлен x²+5*x+8. Значит, x³+9*x²+28*x+32=(x+4)*(x²+5*x+8). Дискриминант уравнения x²+5*x+8 D=5²-4*1*8=-7, поэтому действительных решений это уравнение не имеет. Значит, исходное уравнение имеет лишь два действительных корня: x1=-2 и x2=-4.
ответ: x1=-2, x2=-4.