Необходимо начертить вектор АВ=(2;4) . Начало вектора выбрать произвольно.
Координаты вектора - это проекции вектора на оси ОХ и ОУ. То есть вектор АВ проектируется на ось ОХ в отрезок , длина которого равна 2 единицам, а на ось ОУ - в отрезок, длина которого 4 единицы. Причём, так как координаты положительные, то направление от проекции начала вектора к проекции конца вектора такое же, как и у осей координат.
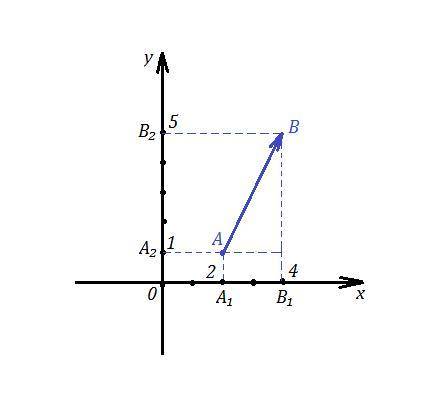
Если , например, за начало вектора возьмём точку А(2,1), то от точки А₁(2,0) , которая является проекцией точки А на ось ОХ, отложим вдоль оси ОХ отрезок длиной 2 единицы в направлении оси ОХ, попадём в точку В₁(4,0), которая будет проекцией точки В на ось ОХ. А₁В₁ - проекция вектора АВ на ось ОХ.
Аналогично, от точки А₂(0,1) отложим вдоль оси ОУ отрезок длиной 4 единицы, попадём в точку В₂(0,5) . А₂В₂ - проекция вектора АВ на ось ОУ.
Затем соединим точку А(2,1) с точкой В(4,5), получим искомый вектор АВ=(2,4).
ответ:
69°
Объяснение:
луч образует прямой угол сс биссектрисой угла а. Что бы найти какой угол образует луч со стороной угла а, нужно из 90° вычесть уголугол, который образовала
биссектриса угла а со стороной угла а. Значит обнимаем из 90° половину 42° и получаем 69°ответ:
69°
Объяснение:
луч образует прямой угол сс биссектрисой угла а. Что бы найти какой угол образует луч со стороной угла а, нужно из 90° вычесть уголугол, который образовала
биссектриса угла а со стороной угла а. Значит обнимаем из 90° половину 42° и получаем 69°
х - 3y = 2
Решение
х = 3y + 2
6( 3y + 2 ) - 3y = 2
18y + 12 - 3y = 2
15y = - 10
y = - 2/3
x = 3•( - 2/3 ) + 2 = - 2 + 2 = 0
ответ ( 0 ; - 2/3 )