Чтобы дробь равнялась 0, надо чтобы числитель равнялся нулю, то есть 2х-5/х=0
Поскольку на 0 делить нельзя, то х не равен нулю, дальше решаем пример. 2х-5=0 х= 5/2
х^2-4/х-2=0 х^2-4=0 х=+-2, но +2 не подходит, поскольку в знаменателе будет 0, а на ноль делить нельзя.
12/7-х=х Найдём ОДЗ - х не должен быть равен 7, дальше умножим части уравнения на (7-х) чтобы избавиться от дроби. Получается 12=(7-х)х
Переносим влево - 12-(7-х)х=0. Раскрываем скобки, решаем уравнение
12-7х+х^2=0 Поменяем порядок, и решим квадратное уравнение
х^2-7х+12=0
х1=3
х2=4
Дана функция 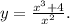
Производная её равна: y' = (3x^2*x^2 - 2x*(x^3 + 4))/x^4 = (x^3 - 8)/x^3.
Приравняем её нулю ( при х не равном 0 можно только числитель).
x^3 - 8 = 0.
x^3 = 8, х = ∛8 = 2. Это критическая точка.
С учётом разрыва функции при х = 0 имеем 3 промежутка монотонности функции: (-∞; 0), (0; 2) и (2; +∞).
На промежутках находим знаки производной.
Находится производная, приравнивается к 0, найденные точки выставляются на числовой прямой; к ним добавляются те точки, в которых производная не определена.
Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
x = -1 0 1 2 3
y' = 9 - -7 0 0,7037.
• Минимум функции в точке: х = 2, у = 3.
• Максимума функции нет.
• Возрастает на промежутках: (-∞; 0) U (2; ∞).
• Убывает на промежутке: (0; 2).
Дано линейное уравнение:
35y - 12 = -15 + y5
Переносим свободные слагаемые (без y5)
из левой части в правую, получим:
35y = y5 + −335y = y5 + −3Переносим слагаемые с неизвестным y5
из правой части в левую:
35y - y5 = -3
Разделим обе части ур-ния на (-y5 + 35y)/y5
y5 = -3 / ((-y5 + 35y)/y5)
Получим ответ: y5 = 3 + 35y
или... 35y−12=
y1=−2.41038137105787
y2=−0.0857144179051239
y3=0.0214119723459405+2.43277054018587i
y4=2.45327184427111
y5=0.0214119723459405−2.43277054018587i
2)
2х=5+6
2х=11
Х= 11:2
Х=5.5