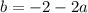
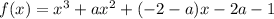
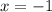, получим 
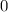, значит корень будет в любом случае равен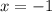 
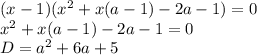Рассмотрим выражение a^2+6a+5=k^2 , так как корни квадратного уравнения имеют вид x1,2=(1-a+/-k)/2 и целыми , то k- должно быть по крайней мере не иррациональным числом . a^2+6a+5 = (a-3)^2-4=k^2 (a+k+3)(a-k+3)=4 , пусть они соотвественно равны x*y=4, рассмотрим случаи x*y={1*4, 4*1, 2*2, -2*-2, -4*-1, -1*-4} по порядку . Первый случай {a+k+3=1 {a-k+3=4 Суммируя оба выражения ,получаем решения a=-1/2, k=-3/2, подставляя в общий вид корня уравнения x1,2 получим не целые значения , рассмотрев аналогично все случаи подходят лишь 1)x=2,y=2 и 2)x=-2,y=-2. При 1) получаем решение a=-1, k=0 2) получаем решение a=-5, k=0 При этом корни целые. Значит a=-1 , b=0 и a=-5, b=8.
x1=x2=4 U x1*x2=-21
x1=-3 U x2=7
x∈(-3;7)