Для того, чтобы выяснить наибольшее число залов, которые можно обойти, не заходя ни в какой зал дважды, нужно правильно раскрасить замок - треугольник. Раскрашиваем в шахматном порядке. Тогда путь по залам - это граф, с вершинами в центрах залов и ребрами - проходами между залами. Видно, ни одно ребро не соединяет вершины одного цвета.
Если начать раскрашивать с первого нижнего углового треугольника в порядке: 1 красим, один - нет, то сумму незакрашенных треугольников можно вычислить по формуле сцммы 1-х n-членов арифметической прогрессии:
а₁=1 (второй верхний ряд треугольников сверху:
а₂=9 (десятый ряд треугольников)
Всего незакрашеные треугольники есть в 9-и рядах, вершина - закрашена)
S₉=(1+9)/2*9=5*9=45 незакрашенных треугольников - залов, значит можно посетить не более 45 незакрашенных залов.
Тогда маршрут может проходить не более, чем по 45+1 закрашенным залам: А - незакрашенный треугольник;
В - закрашенный треугольник.
Маршрут=А+В=А+(А+1)=45+45+1
Маршрут = 91 зал
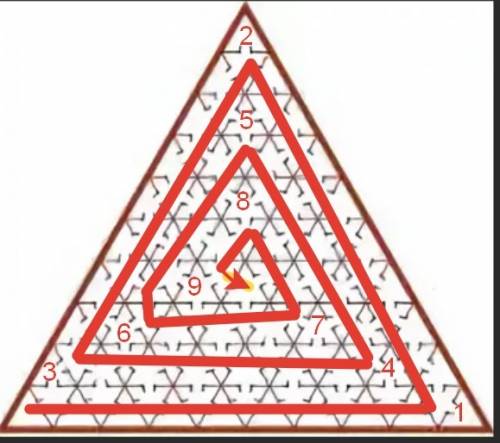
Во вложении 1 - маршрут, который начинается в нижнем левом треугольнике и, продолжаясь по спирали, заканчивается в среднем закрашенном треугольнике, в четвёртом снизу ряду.
Залы, в которые не надо заходить, иначе придется посетить один зал дважды, отмечены чифрами от 1 до 9 по маршруту движения.
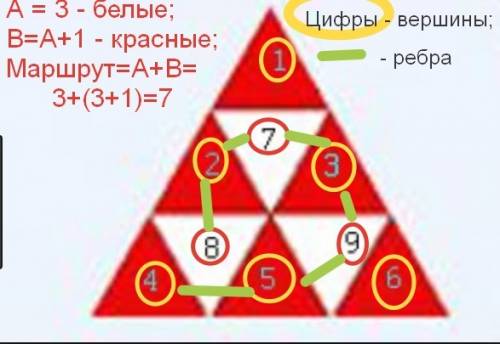
Для наглядности, во вложении 2, пример, подтверждающий формулу, рассмотрен на маленьком треугольнике, разделенном на 9 маленьких.
С практической точки зрения наибольший интерес представляет использование производной для нахождения наибольшего и наименьшего значения функции. С чем это связано? Максимизация прибыли, минимизация издержек, определение оптимальной загрузки оборудования... Другими словами, во многих сферах жизни приходится решать задачи оптимизации каких-либо параметров. А это и есть задачи на нахождение наибольшего и наименьшего значения функции.
Следует отметить, что наибольшее и наименьшее значение функции обычно ищется на некотором интервале X, который является или всей областью определения функции или частью области определения. Сам интервал X может быть отрезком , открытым интервалом , бесконечным промежутком .
В этой статье мы будем говорить о нахождении наибольшего и наименьшего значений явно заданной функции одной переменной y=f(x).