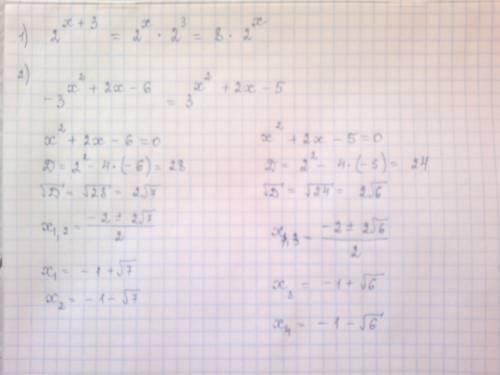
Два поезда выехали одновременно навстречу друг к другу из пунктов А и В. По прибытии в пункт А и В они сразу начали двигаться в обратном направлении. Первый раз они встретились в 180 км от пункта В, а во второй раз в 120 км от пункта А(через 6:00 после первой встречи). Найдите расстояние между пунктами А и В.
Решение
Пусть расстояние между пунктами А и В равно х км.
Заметим, что с момента старта до первой встречи поезда проехали в сумме расстояние, равное х.
С момента старта до второй встречи суммарное расстояние, которое проехали поезда, равно 3х(каждый поезд проезжает между пунктами А и В, и еще одно такуе расстояние они проезжают вдвоем при движении
от пунктов А и В до места второй встречи).
Поэтому время до первой встречи в два раза меньше времени от первой до второй встречи поездов.
Следовательно расстояние преодоленное каждым поездом от момента старта до первой встречи в два раза меньше расстояния,
которое тот же самый поезд проезжает за время между первой и второй встречами.
Составим таблицу из выше приведенного выше решения
Пройденный путь
! 1 встреча! 2 встреча! за 6 ч ! за 3 ч
1 поезд(из В) ! 180 ! х + 120 ! х - 60 ! 180
2 поезд(из А) ! х-180 ! 2х - 120 ! х + 60 ! х-180
Всего ! х ! 3х ! 2х ! х
Пусть до первой встречи 1 поезд проехал 180 км. Тогда между первой и второй встречами он проехал
х – 60 = 2•180.
х - 60 = 360
х = 420 км
ответ: 420 км
1) Если дискриминант квадратного трёхчлена D>0, то квадратное уравнение ax²+bx+c=0 имеет два различных действительных корня.
В этом случае график квадр. трёхчлена - парабола, пересекает ось ОХ в двух точках х₁ и х₂, называемых корнями квадр.трёхчлена.
Причём, если а>0, то у параболы у=ах²+bx+c ветви направлены вверх.
Если же а<0, то ветви направлены вниз.
Соответственно, при решении квадратного неравенства ax²+bx+c>0 в случае D>0 , a>0 будем иметь ответ х∈(-∞,x₁)∪(x₂,+∞) ;
в случае D>0 , a<0 будем иметь х∈(х₁,х₂) , где х₁<х₂ - корни кв. трёхчлена.
См. рис. 1.
2) Если D=0, то квадр. уравнение имеет один корень (а точнее два действительных равных корня х₁=х₂) и квадратный трёхчлен будет представлять из себя полный квадрат: (х-х₁)²=0, х=х₁ .
График квадр. трёхчлена пересекает ось ОХ только в одной точке х=х₁.
При решении неравенства ax²+bx+c>0:
при D=0 , a>0 имеем х∈(-∞,х₁)∪(х₁,+∞) ;
при D=0 , a<0 решений неравенство не будет иметь, т.к. вся парабола расположена ниже оси ОХ, а ниже оси ОХ ординаты отрицательны (у<0),
то есть y=ax²+bx+c<0, либо ах²+bx+с=0 при х=х₁ .
В ответе надо записать: х∈∅ .
См. рис. 2.
3) Если D<0, то квадр. уравнение не имеет действительных корней.
График квадр. трёхчлена НЕ ПЕРЕСЕКАЕТ ось ОХ ни в одной точке,
при а>0 график расположен выше оси ОХ и все у(х)>0,
при а<0 график расположен ниже оси ОХ и все у(х)<0.
При решении квадр. неравенства ах²+bx+c>0:
при D<0 , a>0 имеем х∈(-∞,+∞) , так как какое бы значение "х" мы ни выбрали, соответствующее значение "у" будет положительным (у(х) >0).
при D<0 , a<0 имеем х∈∅, так как при любом значении "х" соответствующее значение "у" будет отрицательным (у(х)=ах²+bx+с<0) .
См. рис. 3.