Объяснение:
Ищем точки пересечения с осью ОХ
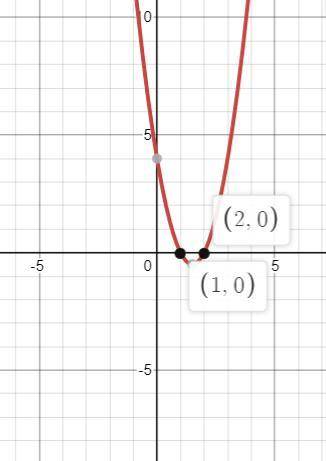
1) Ветви параболы направлены вверх, вершина x₀=-b/2а=6/4=1,5
точки пересечения с осью ОХ:
2x² - 6x + 4=0;
D=36-4*4*2=4; x₁=(6-2)/4;x₁=1;x₂=(6+2)/4;x₂=2
x∈(1;2)
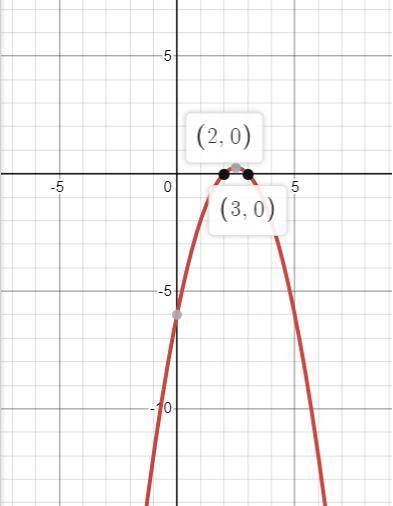
2) Ветви параболы направлены вниз ,вершина x₀=-b/2а=5/2=2,5
точки пересечения с осью ОХ:
x² -5x + 6=0; по т. Виета x₁=2; x₂=3
х∈(-∞;2)∪(3;∞)
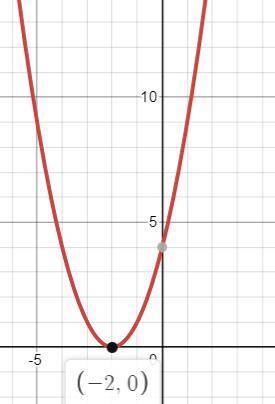
3)y = x² + 4x + 4; y=(х+2)²
y=(х+2)²=0; х=-2. Пересечение в одной точке и это же вершина
х∈∅
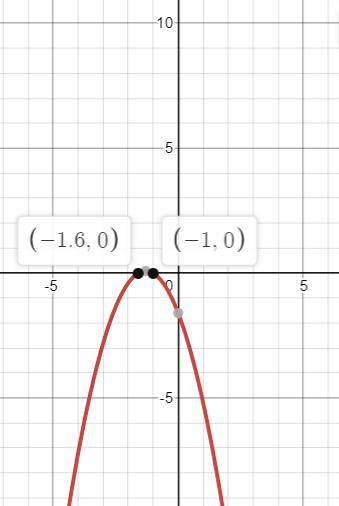
4) Ветви параболы вниз. Вершина x₀=-b/2а=2,6/2=1,3
точки пересечения с осью ОХ: x² + 2,6x + 1,6=0;
По т. Виета x₁=-1,6; x₂=-1.
х∈(-∞;-1,6)∪(-1;∞)
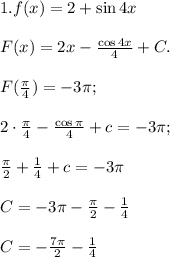
Заданная первообразная -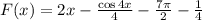 
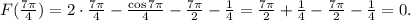
ОТВЕТ: 0.
![2. f(x)=e^x+2x+1, \max_{[0;2]}F(x)=e^2.\\\\F(x)=e^x+x^2+x+C.](/tpl/images/1075/3849/89ce2.png)
График данной первообразная вне зависимости от значения константы на заданном отрезке монотонно возрастает. Поэтому максимальное значение первообразная принимает на правом конце отрезка [0; 2] - т.е. при х = 2.
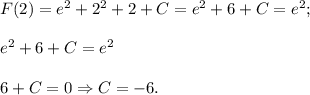
Заданная первообразная -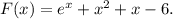 
Соответственно все из того же факта монотонного возрастания следует и то, что минимальное значение первообразная принимает на левом конце отрезка [0; 2] - т.е. при х = 0.
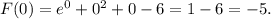
ОТВЕТ: -5.
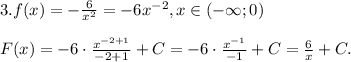
По условию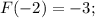 
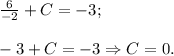
Заданная первообразная -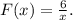 
Решим уравнение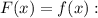 
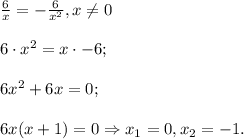
Однако вспоминаем про ограничение для самой переменной: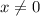 
(о чем прописано также и в условии существования первообразной). Делаем вывод: уравнение имеет единственное решение 
ОТВЕТ: {-1}.
