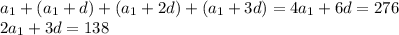
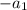 при делении на 3, значит разность
при делении на 3, значит разность  дает остаток
дает остаток 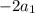 при делении на 3, но их разность кратна 3. Поэтому первое число кратно 3.
при делении на 3, но их разность кратна 3. Поэтому первое число кратно 3.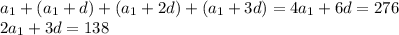
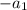 при делении на 3, значит разность
при делении на 3, значит разность  дает остаток
дает остаток 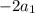 при делении на 3, но их разность кратна 3. Поэтому первое число кратно 3.
при делении на 3, но их разность кратна 3. Поэтому первое число кратно 3.
2cos²x=1
cos²x=1/2
cosx=1/√2 cosx= - 1/√2
cosx=√2/2 cosx= - √2/2
x=(+/-) π/4 + 2πk, k∈Z x=(+/-) 3π/4 + 2πk, k∈Z
ответ: (+/-) π/4 + 2πk, k∈Z;
(+/-) 3π/4 + 2πk, k∈Z.
2) sin2t=2sintcost
Исходя из того, что cost= -5/13, то угол t лежит или во второй
четверти, где sint имеет знак "-"; или лежит в третьей четверти,
где sint имеет знак "+". В условии это условие не указано. Поэтому
рассмотрим два случая:
1) угол t лежит во второй четверти, то есть
π/2 < t < π
sint= -√(1-cos²t) = -√(1 - (-5/13)²) = -√(1 - ²⁵/₁₆₉) = -√(¹⁴⁴/₁₆₉) = -12/13
sin2t=2 * (-12/13) * (-5/13) = 120/169
2) угол t лежит в третьей четверти, то есть
π < t < 3π/2
sint= √(1-cos²t) = √(1 - (-5/13)²) = √(1 - ²⁵/₁₆₉) = √(¹⁴⁴/₁₆₉) = 12/13
sin2t=2 * (12/13) * (-5/13) = - 120/169