Так как в уравнении есть квадратные корни, то запишем ОДЗ:
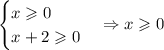
Также заметим, что в левой части записано произведение двух неотрицательных выражений. Значит, правая часть уравнения также неотрицательна:
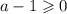
Таким образом, при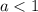 
уравнение не имеет корней.
Предположим, что . Тогда:
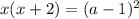
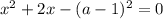
Проверим, удовлетворяют ли найденные корни ОДЗ.
Для первого корня получим:
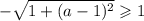
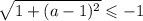
Однако, квадратный корень не может принимать отрицательных значений. Значит, рассматриваемое выражение не является корнем уравнения ни при каких значениях параметра 
.
Для второго корня получим:
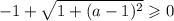
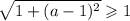
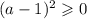
Последнее условие выполняется при любых значениях параметра . Но как отмечалось ранее, уравнение может иметь корни только при . Значит, данное выражение является корнем уравнения при .
при 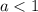: нет корней,
при : 
Решение
Через вершину B проведем прямую, параллельную AC, продлим медиану AА₁ до пересечения с этой прямой в точке T.
Из равенства треугольников А₁BT и A А₁C (по стороне и двум прилежащим углам: B А₁ = А₁C, т. к. A А₁ — медиана,
∠B А₁T = ∠A А₁C — вертикальные, ∠ А₁BT = ∠ А₁CA — накрест лежащие при параллельных прямых AC, BT и секущей BC) следует, что BT = AC и A А₁ = KT. Из подобия треугольников
AML и MBT (по двум углам: ∠MAL = ∠BTА₁,
∠ALB = ∠LBT — накрест лежащие при параллельных
прямых AC, BT и секущих BL, AT) следует,
что AL : BT = AL : AC = AM : MT. Так как АА₁ = А₁T,
то AM : MT = 1 : 7.
Тогда AL : AC = 1 : 7, а AL : LC = 1 : 6.
решение во вкладыше
