y(x) = (x + x^2/2 + C)(1+x)^2
Объяснение:
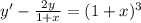
Это неоднородное уравнение, решается заменой:
y(x) = u(x)*v(x), тогда y'(x) = u'(x)*v(x) + u(x)*v'(x)
 (1)
(1)
Вынесем за скобки всё, что можно. У нас это только u:
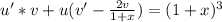 (2)
(2)
Скобку в левой части приравняем к 0:

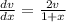

Получили уравнение с разделёнными переменными, интегрируем:
ln |v| = 2ln |1+x| = ln (1+x)^2
v(x) = (1+x)^2
Подставляем в уравнение (2):
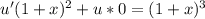
Делим всё уравнение на (1 + x)^2:
u' = 1 + x
Интегрируем:
u(x) = x + x^2/2 + C
Делаем обратную замену:
y(x) = u(x)*v(x) = (x + x^2/2 + C)(1+x)^2
ОДЗ-Обдщее Дозволенное Значение
Объяснение:
ну одз это типо что может быть дозволенно. Под корнем вот нельзя чтобы было отрицательное число. 2х-3 больше либо равно 0
х значит больше либо равно 1,5. если х будет меньше 1,5 то под корнем будет отриц число,а это пустое множество.
ну вот. а для уравнения пример покажу 6√2х-3 = 1. обе части возводим в 6ую степень. 1⁶ это все равно 1. значит 2х-3=1. 2х=1+3. 2х=4 х=2. вместо 1ого любое число может быть,надо просто его в 6ую степень возвести,ну или на любое число которое гад знаком корня стоит
2) 4x² + 5x - 9x² + 15x = - 5х² + 20х = 5х (4 - х)
3) 4x² - 4y² + 3x + 3y = 4 (х² - у²) + 3 (х + у) = 4 (х - у)(х + у) + 3 (х + у) = (4х - 4у + 3)(х + у)