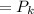 , то остается вычислить вероятности того сколько самолётов собют системы ПВО.
, то остается вычислить вероятности того сколько самолётов собют системы ПВО.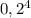
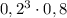
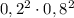
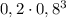
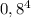 - логика подсказівает, что если самолеты были сбиты системой ПВО то соответствующая вероятность попадания
- логика подсказівает, что если самолеты были сбиты системой ПВО то соответствующая вероятность попадания 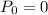 но как по мне это не наше дело, нам ничего не мешает оставить это слагаемое в формуле, в результате получим:
но как по мне это не наше дело, нам ничего не мешает оставить это слагаемое в формуле, в результате получим: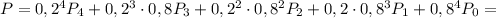
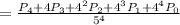
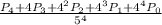
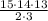
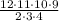
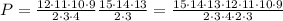
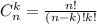
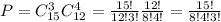
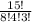
База индукции: 1
Предположим, что утверждение верно для n=k.
Покажем, и докажем, что утверждение верно так же для n=k+1.
Так как , следуя предположению
Т.е. предположение верно. Ч.Т.Д.
2)
База : 1
Проверка:
Предположение:
Теперь покажем и докажем, что данное выражение верно и при
Так как предыдущий член был равен k, то что бы узнать сумму первых k+1 членов, достаточно прибавить k+1 член (используя формулу которую мы доказали ранее):
т.е. мы пришли к изначальной формуле, если туда подставить k+1. Ч.Т.Д.
3)
Это не формула общего члена, это формула суммы.
При
База: 1
Предположим, что формула верна для:
Покажем и докажем что формула верна для
Как и с суммой арифм.прогрессии. Мы добавим k+1 член к сумме.
Ч.Т.Д.