Объяснение:
Квадратичная функция: f(x) = ax²+ bx + c
Дана функция:
f(x) = 3 + 2x - x² или f(x) = -x² + 2x +3
- парабола, ветви вниз (a<0)
Найдем координаты вершины:
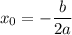 - ось симметрии.
- ось симметрии.
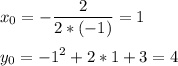
⇒ координаты вершины (1; 4)
Пересечение с осями:
1) с осью 0у ⇒
х = 0; у = 3.
2) с осью 0х ⇒
у=0; -х² +2х +3 = 0
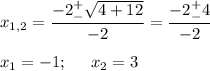
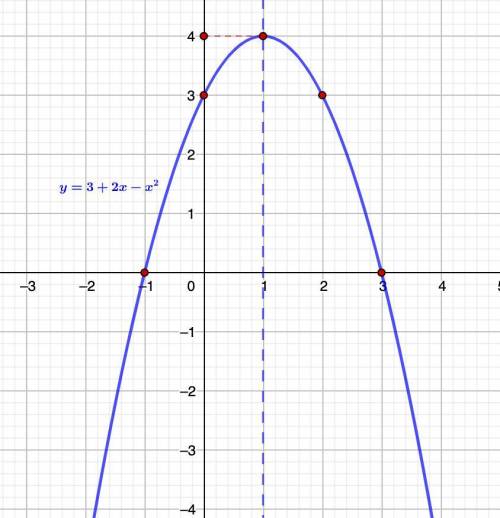
Строим график (см. рис)
По графику определим:
1) f(x) > 0 (часть графика выше оси 0х)
f(x) > 0 при х ∈ (-1; 3)
f(x) < 0 (часть графика ниже оси 0х)
f(x) < 0 при х ∈ (-∞; -1) ∪ (3; +∞)
2) Область значения функции
Е(у) : y ∈ (-∞; 4]
3) Промежутки возрастания и убывания функции:
Возрастает (при увеличении значений х, значения у тоже увеличиваются) при
х ∈ (-∞; 1]
Убывает (при увеличении значений х, значения у уменьшаются) при
х ∈ [1; +∞)
Я в тебя верю, станешь пилотом!
А вот я для тебя решил
А) Тянем первый билет, с вероятностью 3/15 = 1/5 мы вытянем выигрышный билет. Значит, осталось 14 билетов, среди которых уже 2 выигрышных билета. Тянем второй раз, вероятность вытянуть выигрышный билет равна 2/14 = 1/7. Следовательно, вероятность два раза подряд вытащить выигрыш равна 1/5 * 1/7 = 1/35.
б) Здесь надо рассмотреть два случая.
В первый раз вытаскиваем выигрыш (вероятность 3/15=1/5), во второй раз - нет (вероятность 12/14=6/7). Вероятность такой ситуации 1/5 * 6/7 = 6/35.
И другой случай, сперва вытаскиваем билет без выигрыша (вероятность 12/15=4/5), а во второй раз с выигрышем (вероятность 3/14). Вероятность этой ситуации 4/5 * 3/14 = 12/70 = 6/35
Суммируем вероятности обоих случаев 6/35 + 6/35 = 12/35
в) В первый раз не вытянули билет с выигрышем (вероятность 12/15=4/5) и во второй раз (вероятность 11/14). Итоговая вероятность такого варианта развития событий - 4/5 * 11/14 = 22/35
15с-10с^2=5с(3-2с)