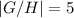
Объяснение:
По определению факторгруппы, "a" эквивалентно "b" тогда и только тогда, когда 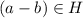
Выберем какой-нибудь элемент группы 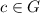 . Подсчитаем, сколько элементов из группы эквивалентно этому элементу
. Подсчитаем, сколько элементов из группы эквивалентно этому элементу
Понятно, что таких элементов ровно 4 штуки:
-- 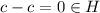
-- 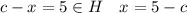
-- 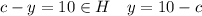
-- 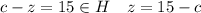
Докажем, что например 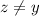
Действительно, иначе было бы 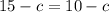
Отсюда 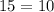 , что попросту неверно в
, что попросту неверно в 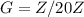
Аналогично рассматриваются другие случаи. Таким образом, любому элементу 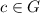 эквивалентно ровно 4 элемента группы G(включая сам элемент
эквивалентно ровно 4 элемента группы G(включая сам элемент  ). К тому же, в группе
). К тому же, в группе 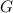 содержится 20 элементов
содержится 20 элементов
Таким образом, в факторгруппе содержится 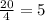
1-779/781=781/781 -779/781=2/781
теперь сравним 2/993 < 2/781
т.е 991/993 до целой единицы требуется меньшей добавки, чем779/781
следовательно оно больше
991/993>779/781