|x² - 16| + |x + 2| = 14 - x - x²
|(x - 4)(x + 4)| + |x + 2| = 14 - x - x²
x₁ = 4 ; x₂ = - 4 ; x₃ = - 2
1) x ∈ (- ∞ ; - 4)
x² - 16 -x - 2 = 14 - x - x²
2x² = 32
x² = 16
x₁ = - 4 - неуд
x₂ = 4 - неуд
2) x ∈ [ - 4 ; - 2)
- x² + 16 - x - 2 = 14 - x - x²
- x² - x - x + x² = 14 - 14
0 * x = 0
ответ : x ∈ [ - 4 ; - 2)
3) x ∈ [ - 2 ; 4)
- x² + 16 + x + 2 = 14 - x - x²
- x² + x + x + x² = 14 - 18
2x = - 4
x = - 2
4) x ∈ [4 ; + ∞)
x² - 16 + x + 2 = 14 - x - x²
x² + x + x + x² - 14 - 14 = 0
2x² + 2x - 28 = 0
x² + x - 14 = 0
D = 1² - 4 * (- 14) = 1 + 56 = 57
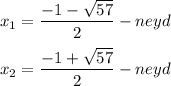
- 4 + (- 3) + (- 2) = - 9
ответ : - 9

В один круг это означает, что каждая команда может сыграть с любой другой командой не более 1 раза? Если да, то:
У одной команды число сыгранных матчей должно быть не более 17-ти. Пусть в какой-то момент НЕ найдутся две команды, сыгравшие одинаковое число игр.
У всех команд должны быть разное количество сыгранных матчей. Необходимо 18 разных цифр - кол-во матчей у всех команд. При этом эти цифры должны находиться в отрезке [0;17]. Единственный доступный вариант, удовлетворяющий данным условиям, - ряд идущих подряд цифр от 0 до 17.
Если одна из команд сыграла 17 матчей, то она должна была сыграть со всеми командами хотя бы по одному разу. А мы видим, что одна из команд не сыграла ни одного матча.
Мы использовали метод "от противного" и пришли к логическому противоречию. Это означает, что в любой момент найдутся две команды,сыгравшие одинаковое число игр.
Извиняюсь за тяжелое, возможно, для восприятие решение.