Пусть моркови было х кг.
Тогда картофеля было 2,5х кг, а лука 2,5х+14 кг.
Всего овощей на базе было х+2,5х+2,5х+14 кг, что по условию задачи равно 590 кг.
х+2,5х+2,5х+14=590
6х=590-14
х= 576:6
х=96 (кг)- морковь
2,5*96=240 (кг) - картофель
2,5*96+14 =254 (кг) лук
А вторая задача правильно задана, в смысле все условия вышеперечислены?
Пусть скорость катера х км/ч, тогда по расстояние из А в В было 8*(х+2) км - 8 это время, 2 это скорость течения реки, ну а формулу расстояния знают все :время *на скорость
А расстояние Из В в А составляет 9*(х-2) - минус Т.К. против течения. Так как расстояния туда и обратно равны составляем уравнение
9*(х-2) = 8*(х+2)
9х-18 =8х+16
9х-8х=18+16
1х=34 Км/ч - скорость катера
Окружность с центром в т. O и D = 68. Хорда AB.
Расстояние OM = 30 от т. O до прямой AB.
Найти:AB - ?
Решение:Заметим, что OM ⊥ AB (так как OM - это расстояние от т. О до прямой AB - длина перпендикуляра из точки О к прямой AB).
Пусть отрезок OM лежит на радиусе OC рассматриваемой окружности. Тогда OC, как радиус, перпендикулярный хорде, пересекает эту хорду ровно в ее середине: AM = BM.
Рассмотрим прямоугольные треугольники, равные по первому признаку (или же по двум катетам OM = OM и AM = BM): ΔAOM = ΔBOM.
OA = OB = D / 2 = 68 / 2 = 34, как радиусы.
OM = 30, по условию.
Применим теорему Пифагора, например, к ΔAOM:
AM² + OM² = AO²
AM² = AO² - OM²
AM² = 34² - 30²
AM² = 256
AM = 16
Значит:
AB = AM + BM = AM + AM = 16 + 16 = 32.
Задача решена!
ответ: 32.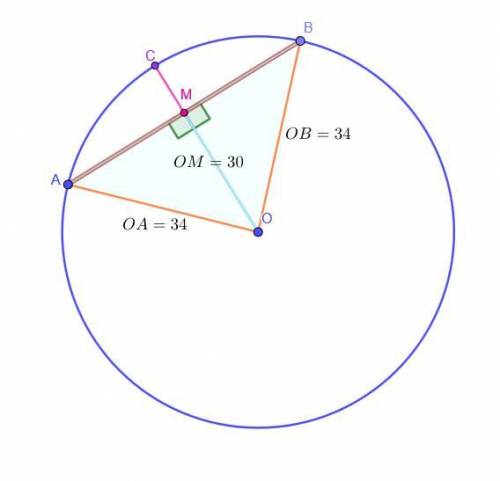
4/7 х- количество батончиков
х-8=4/7х+1
х-4/7х=9
3/7х=9
х=21 карамелька
21*4/7=12 батончики
21+12=33 конфеты