y = x³ - 4x²
Найдём производную :
y' = (x³)' - 4(x²)' = 3x² - 8x
Найдём критические точки, для этого приравняем производную к нулю.
y' = 0
3x² - 8x = 0
x(3x - 8) = 0
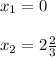
Отметим критические точки на числовой прямой и выясним знаки производной на промежутках, на которые эти точки разбивают числовую прямую .
y'(x) + - +
____________0___________2 2/3_____________
y(x) ↑ ↓ ↑
На промежутках (- ∞ ; 0] и [2 2/3 ; + ∞) -функция возрастает
На промежутке [0 ; 2 2/3] - функция уюывает
Увеличиваем длину на 1 и, соответственно, уменьшаем на 1 ширину:
S = (a+1)(a-1) = a² - 1 = 625 - 1
Увеличиваем длину на 2 и уменьшаем на 2 ширину:
S = (a+2)(a-2) = a² - 4 = 625 - 4 и т.д.
Таким образом, максимальная площадь прямоугольника с заданным периметром будет у квадрата.