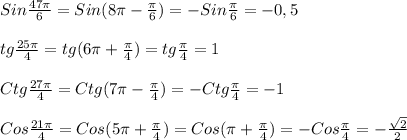
1222234567890-=-09876543
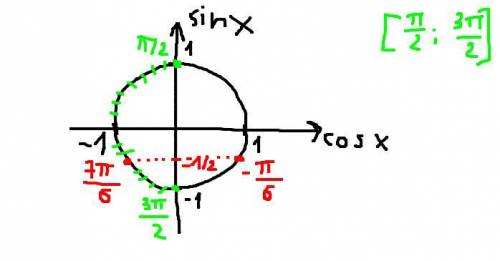
![Объясните, как это решать? ! sin\frac{47\pi }{6} tg\frac{25\pi }{4} ctg\frac{27\pi }{4} [tex]\frac{2](/tpl/images/3212/1080/1e88b.jpg)
Парабола и прямая пересекаются в двух точках: (-20;80) и (5;5).
Объяснение:
Парабола y = 1/5x2 и прямая y = 20 - 3x пересекаются, если эта система имеет решение.
y = 1/5x2,
y = 20 - 3x;
1/5x2 = 20 - 3x;
1/5x2 + 3x - 20 = 0 (умножим на 5);
5x2 + 15x - 100 = 0;
Легко найти корни по теореме, обратной теореме Виета (можно и по формуле корней).
x1 = -20, x2 = 5.
Тогда y1 = 20 - 3 * (-20) = 20 + 60 = 80,
y2 = 20 - 3 * 5 = 20 - 15 = 5.
Парабола и прямая пересекаются в двух точках: (-20;80) и (5;5).
x = 7 /6
/6
Объяснение:
2 sin x = -1
sin x = -0.5
Отмечаем нужные точки на тригонометрическом круге
Это x = - /6 + 2
/6 + 2
Так же можно задать это множество решений так:
x = 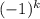 * (-
* (-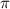 /6) +
/6) +
Нам нужно выбрать из множества решений только те, которые принадлежат заданному промежутку.
Отметим этот промежуток на тригонометрическом круге
Из рисунка видно, что подходит только одно решение x = 7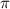 /6
/6
Это решение можно было найти другим решив неравенство
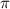 /2
/2 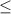 x
x
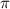 /2
/2 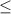 7
7
1/2 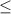 7/6 + 2k
7/6 + 2k
3  7 + 12k
7 + 12k
Так как k - целое, то подходит только k = 0, при других целых k неравенство не выполняется.
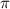 /2
/2 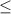 -
-
1/2 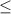 -1/6 + 2k
-1/6 + 2k
3  -1 + 12k
-1 + 12k
Здесь нет целых значений k, для которых бы выполнялось неравенство (при k = 0 -1+0<3, при k = 1 -1+11>9)
Значит, решением является только x = 7 /6
/6
Но здесь проще находить решение именно из тригонометрического круга по рисунку.