91
Объяснение:
Какое наименьшее количество различных трехзначных чисел нужно взять, чтобы среди них наверняка было бы одно число, оканчивающееся НЕ на нуль - на одно больше чем количество различных трехзначных чисел оканчивающееся на нуль
Найдем количество различных трехзначных чисел оканчивающееся на нуль, последняя цифра 0 (1 вариант выбора), первая любая цифра от 1 до 9 (9 вариантов выбора), вторая - любая цифра от 0 до 9 (10 вариантов выбора), по правилу умножения событий, получаем что всего таких чисел 9*10*1=90
а значит нужно 91 число (90+1=91)
Решите уравнение
(X+1)^2/3-(X-1)/2=(8X-1)/6
(X+1)^2/3-(X-1)/2=(8X-1)/6 |*6
2(X+1)^2-3(X-1)=8X-1
2x^2+4x+2-3x+3-8x+1=0
2x^2-7x+6=0
D=49-4*2*6=1
x=1,5
x=2
Решите уравнение
(2X-3)^2-2(5X-4)(X+1)=-9-13X
(2X-3)^2-2(5X-4)(X+1)=-9-13X
4x^2-12x+9-2(5x^2+5x-4x-4)+9+13x=0
4x^2-12x+9-10x^2-10x+8x+8+9+13x=0
6x^2+x-26=0
D=1-4*6*(-26)=625
x=-13/6
x=2
Не вычисляя корней квадратного уравнения, решите уравнение
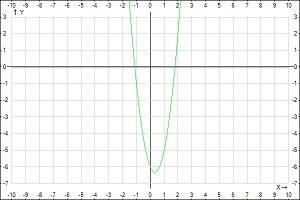
1) 3X^2-2X-6=0
y(первое)=3X^2-2X-6
y(второе)=0
найдем координаты вершины параболы:
x(в)=-b/2a=2/6=1/3
y(в)=3(1/3)^2-2(1/3)-6=-19/3
координаты:(-19/3)
2. 5.6-7.04 = -1.44
3. 15,4-1,44=13.96
ответ 13.96