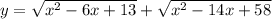
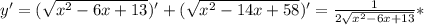
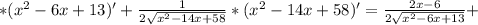
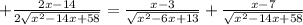
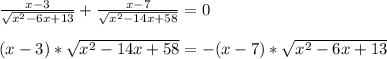
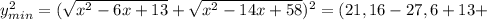
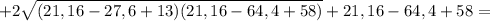

Для отыскания наибольшего(наименьшего) значения функции существует один и тот же приём:
1) ищем производную.
2) приравниваем её к нулю и ищем корни.
3) смотрим , какие корни входят в указанный промежуток.
4)ищем значения данной функции на концах указанного промежутка и в точках, входящих в указанный промежуток.
5) пишем ответ.
Начали.
y = x³ -3x² +7x -5 [1;4]
y' = 3x² -6x +7
3x² -6x +7 = 0
D<0 корней нет
х = 1
у = 3*1² -6*1 +7 *1 -5 = -1
х = 4
у = 3*4³ -3*4²+7*4 -5 = 192 - 48 +28 -5 = 163
ответ: max y = 163
min y = -1
x^2+t^2=|x+t|+|x-t|
построим графики функций у=x^2+t^2; y=|x-t|; y=|x+t|
по оси х отмечаем -t I t; по оси у; t^2;|t|
строим параболу( вершина (0:t^2) и |x|; -|x| -то углы с вершиной (-t;0) i (t;0)
t^2=2|t|
t>0; t^2=2t; t^2-2t=0; t(t-2)=0; t=0 ili t=2
a-1=2; a=3
если t=0,
x^2+(1-1)^2=|(x-1+1|+|x-1+1|
x^2=2|x| два корня, а=1-не подходит
t<0; t^2=-2t; t^2+2t=0; t=0 ili t=-2
a-1=-2; a=-1
ответ. -1;3
,