При каких значениях a неравенство имеет не менее пяти целочисленных решений х²+у²-а²≤6х-4у+а-13.
Объяснение:
х²+у²-а²≤6х-4у+а-13 ,
х²-6х+у²+4у≤а²+а-13 ,
х²-6х+9-9+у²+4у+4-4≤а²+а-13 , свернем формулы
(х-3)²+(у+2)²≤а²+а-13 +13 ,
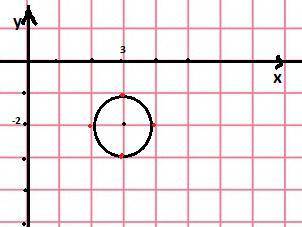
(х-3)²+(у+2)²≤а²+а . Данное неравенство ограничивает часть плоскости внутри круга с центром (3;-2) . Если r=1 , то целочисленных решений пять ( четыре лежат на окружности и одно в центре) . Значит радиус r≥1 или r²≥1.
Выражение а²+а =r² и тогда а²+а≥1 , а²+а-1≥0 . Нулями данного квадратного трехчлена являются значения :
а₁=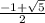
, а₂=
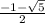. Метод интервалов :
+++++++[ ]- - - - - -[ ]+++++++. ⇒
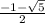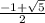х∈(-∞ ;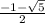 ] и [ ; +∞).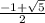
При каких значениях a неравенство x² +y²- a²≤ 6x - 4y+a -13 имеет не менее пяти целочисленных решений ?
ответ: a ∈ (-∞ ; (-1 -√5)/2 ] ∪ [-1 +√5)/2 ; ∞)
Объяснение:
x² +y²- a²≤ 6x - 4y+a -13 ⇔(x²- 6x+9+y²) +(4y +4 )≤ a² + a ⇔
(x -3)²+ (y + 2)² ≤ a² + a. || Ясно (x -3)²+ (y + 2)² ≥ 0 , значит неравенство имеет решений, если a² + a ≥ 0 ⇔ (a+1)a ≥0 ⇒ a∈( -∞ ;-1]∪ [0 ;∞). ||
если a = -1 или a =0 → одно решение: (3 ; -2 ) .
(x -3)² + (y + 2)² = R² уравнения окружности с центром в точке (3 ;-2)
и радиусом R .
Решение нераенства (x -3)² + (y + 2)² ≤ a² +a точки круга с центром в точке (3 ;-2) и радиусом R =√a(a+1) .
R = 1 ровно пять целочисленных решений ,
R =√2 → 9 целочисленных решений
имеет не менее пяти целочисленных решений , если
R² = a² +a ≥ 1⇔ a² + a - 1 ≥ 0 ⇒ a ∈ (-∞ ; (-1 -√5)/2 ] ∪ [-1 +√5)/2 ; ∞) .
2 слога: трава мельник
3 слога: теремок ягода