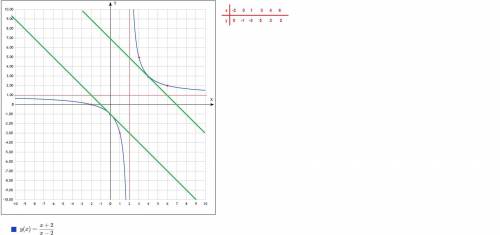
y=1-4/(x-2)-это гипербола y=-1/x во второй и четвертой четверти со сдвигом по оси y на 1 единицу вверх и сдвигом по оси х на 2 единицы вправо
тангенс угла наклона равен производной функции в точке
y`=((x-2)-(x+2))/(x-2)^2= -4/(x-2)^2
tg(-pi/4)=-1
-4/(x-2)^2=-1
(x-2)^2=4
x-2=2; x1=4; y1=(4+2)/(4-2)=3
x-2=-2; x2=0;y2=(0+2)/(0-2)=-1
(4;3); (0;-1)-искомые точки
Объяснение:
составим систему уравнений
b(5)-b(3)=1200 (1)
b(5)-b(4)=1000 (2) ⇒ b(5)= 1000+b(4) (2_2)
Добавим в систему третье уравнение b(4)²=b(5)*b(3) (3)
вычтем из уравнения (1)-(2) ⇒ b(4)-b(3)=200 ⇒ b(3)=b(4)-200 (4)
Подставим (2_2) в (3)
b(4)²=(1000+b(4))*b(3) Подставим вместо b(3) уравнение (4)
b(4)²=(1000+b(4))*(b(4)-200)
b(4)²==1000b(4)+b(4)²-200000-200b(4) [b(4)² сократим]
800 b(4)=200000 b(4)=250
b(3)=250-200=50 b(3)=50
q=b(4)/b(3)=250/50=5 q=5
b(3)=b(1)*q² ⇒ b(1)=50/25=2 b(1)=2
S(5)= b(1)(q^n-1)/(q-1)
S(5)=3125
аn = - 0,3n + 1.
Объяснение:
1) аn = - 0,3n + 1;
а(n+1)= - 0,3(n+1) + 1 = - 0,3n - 0,3 + 1 = - 0,3n + 0,7;
а(n+1) - an = - 0,3n + 0,7 - (- 0,3n + 1) = 0,7 - 1 = - 0,3.
Каждый последующий член последовательности, начиная со второго, равен предыдущему, сложенному с одним и тем же числом d = - 0,3. Последовательность является прогрессией.
2) аn = 4 - n³
a1 = 4 - 1 = 3;
a2 = 4 - 8 = -4;
a3 = 4 - 27 = - 23.
а2 - а1 = - 7 не равно а3 - а2 = -19, последовательность арифметической прогрессией не является.
3) аn = (-2)^n
а1 = (-2)^1 = - 2;
а2 = (-2)^2 = 4;
а3 = (-2)^3 = - 8;
а2 - а1 = 6 не равно а3 - а2 = -12, последовательность арифметической прогрессией не является.
4) an = 1 + 3/n
a1 = 1 + 3/1 = 4;
a2 = 1 + 3/2 = 2,5;
a3 = 1 + 3/3 = 2;
а2 - а1 = -1,5 не равно а3 - а2 = - 0,5, последовательность арифметической прогрессией не является.
Решение во вложении. Удачи.
ответ : (0;-1)v(4:3)