1)
ОДЗ: 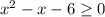 ⇒
⇒ 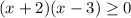 ⇒
⇒ ![x \in (-\infty; -2] \cup [3;+\infty)](/tpl/images/1361/5355/f678f.png)
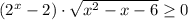 ⇔
⇔
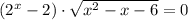 или
или 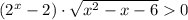
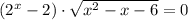 ⇒
⇒ 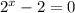 или
или 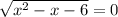 ⇒
⇒
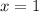 или
или  или
или 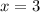
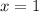 не входит в ОДЗ
не входит в ОДЗ
два корня  или
или 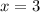
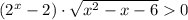 при
при ![x \in (-\infty; -2] \cup [3;+\infty)](/tpl/images/1361/5355/f678f.png)
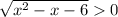 , тогда
, тогда 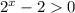 ⇒
⇒ 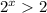 ⇒
⇒ 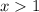
C учетом ![x \in (-\infty; -2] \cup [3;+\infty)](/tpl/images/1361/5355/f678f.png) получаем ответ:
получаем ответ:
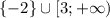
2)
ОДЗ: 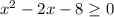 ⇒
⇒ 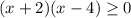 ⇒
⇒ ![x \in (-\infty; -2] \cup [4;+\infty)](/tpl/images/1361/5355/4ed2b.png)
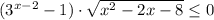 ⇔
⇔
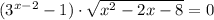 или
или 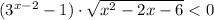
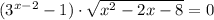 ⇒
⇒ 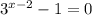 или
или 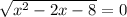 ⇒
⇒
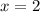 или
или  или
или 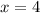
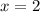 не входит в ОДЗ
не входит в ОДЗ
два корня  или
или 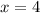
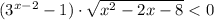 при
при ![x \in (-\infty; -2] \cup [4;+\infty)](/tpl/images/1361/5355/4ed2b.png)
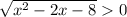 , тогда
, тогда 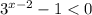 ⇒
⇒ 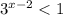 ⇒
⇒ 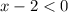
C учетом ![x \in (-\infty; -2] \cup [4;+\infty)](/tpl/images/1361/5355/4ed2b.png) получаем ответ:
получаем ответ:
![(-\infty;-2]\cup \{2\}](/tpl/images/1361/5355/83f26.png)
3)
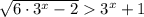
Так как 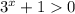 при любых х, возводим данное неравенство в квадрат:
при любых х, возводим данное неравенство в квадрат:
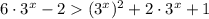
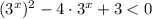
D=16-12=4
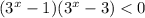
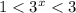
Показательная функция с основанием 3 возрастает
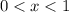
О т в е т. (0;1)
4)

Так как 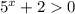 при любых х, возводим данное неравенство в квадрат:
при любых х, возводим данное неравенство в квадрат:
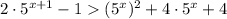
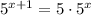
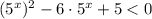
D=36-20=16
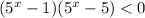
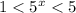
Показательная функция с основанием 5 возрастает
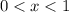
О т в е т. (0;1)
1.
(x+7)(x-2)=x² - 2x+7x - 14=x²+5x-14
(y+5)(y²-3y+8)=y³-3y²+8y+5y²-15y+40=y³+2y² - 7y+40
(4c-d)(6c+3d)=24c²+12cd-6cd-3d²=24c²+6cd-3d²
2.
y(a-b)+2(a-b)=(a-b)(y+2)
3x-3y+ax-ay=3(x-y)+a(x-y)=(x-y)(3+a)
3.
xy(x+y)-(x²+y²)(x-2y)=x²y+xy² - (x³-2x²y+xy²-2y³)=x²y+xy²- x³+2x²y-xy²+2y³=2y³+3x²y - x³
4.
a(a-2)-8=(a+2)(a-4)
a²-2a-8=a²-2a-8
0=0 - верно
5.
х дм - ширина прямоугольника
х+12 (дм) - длина
х+12+3 (дм) - увеличенная длина
х+2 (дм) - увеличенная ширина
х(х+12)=(х+12+3)(х+2)-80
х²+12х=х²+17х+30-80
17х-12х=50
5х=50
х=10(дм) - ширина прямоугольника
10+12=22(дм) - длина
y'=[1/x^(1/3)]-1=0=>x=1. y'>0=>xє(0;1). y'<0=>xє(1;+oo).
f(1)=1/2. (1;1/2)- точка максимума- наибольшее значение функции на интервале (0;8). Слева функция не определена в точке х=0, поэтому ищем правосторонний предел данной функции при х->0; lim(3/2*x^(2/3)-x)=0.
Слева наименьшее значение у=0. Справа: y(8)=3/2*8^2/3-8=-2.
ответ: Fmax=1/2, Fmin=-2.