Вариант Б1:
1Дано:
АО=DO
<1=<2
Док-ть: тр. АОВ=тр. DOC
Доказательство:
1) <ВАО+<1 = 180° (смежные)
<CDO+<2 = 180° (смежные)
<ВАО = 180 - <1
<CDO = 180 - <2
Т.к. <1 и <2 равны (по усл.), то:
<BAO=<CDO
2) Рассмотрим тр-ки AOB и DOC:
<BAO=<CDO (доказано)
<BOA = <COD (вертик.)
AO=DO (по усл.)
Значит,
тр AOB = тр DOC
Доказано.
2Дано:
ABCD — четырехугольник
AD=BC, AB = CD
Доказать: <А = <С
Доказательство:
1) Доп. построение — диагональ BD
2) Рассм. тр-ки ABD и CBD:
AD = BC, AB = CD (по усл.)
BD — общая.
Значит,
тр ABD = тр CBD
3) В равных треугольниках все соответствующие элементы равны.
Значит,
<A = <C
<A = <CДоказано.
3Дано:
ABCD — четырёхугольник
BD, AC — диагонали.
тр ABC = тр CDA
Доказать: тр ABD = тр CDB
Доказательство:
1) Т. к. тр-ки ABC и CDA равны, то:
AD = BC
AB = CD
2) Рассмотрим тр-ки ABD и CDB:
AD = BC, AB = CD (док.)
BD — общая
Значит,
тр ABD = тр CDB
Доказано.
Решением является перебор вариантов:
Можно достать шары из урны четырьмя
1) 2 белых
2) 2 чёрных
3) 1 белый и 1 чёрный
4) сначала 1 чёрный, потом 1 белый.
Вероятности этих событий:
1) 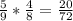
2) 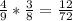
3) 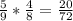
4) 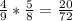
Вероятность того, что мы достанем из урны два одинаковых по цвету шара равна сумме вероятностей в первом и во втором случаях:
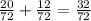
Вероятность вынимания шаров разных цветов (не важно в какой последовательности) равна сумме вероятностей в третьем и в четвёртом случаях:
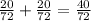
Сравнивая две полученные дроби мы приходим к выводу, что вынуть два разных по цвету шара более вероятнее, чем два одинаковых.