Объяснение:
СМЕНА ЗНАКА В НЕРАВЕНСТВАХ
И логарифмическая, и показательная функция могут быть либо монотонно убывающей (при основании < 1 ), либо монотонно возрастающей ( при основании больше 1 ). Если функция является монотонно возрастающей, тогда ее значение будет тем больше, чем больше аргумент. Поэтому, если основание логарифма или основание показательной функции больше 1, то при снятии логарифма или экспоненты знак неравенства сохраняется. Если функция монотонно убывает, то ее значение тем меньше, чем больше аргумент. Поэтому, при основании меньше 1 знак неравенства изменяется на противоположный.
Это очень важное свойство, о котором, тем не менее, очень часто забывают.
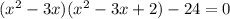
1. х-2 больше или равно нуля, то есть х больше или равно 2.
в этом случае скобки модуля просто снимаются:
х-1-(х-2)=1
х-1-х+2 =1
2х+1=1
2х=0
х=0 -- корень не входит в область определения (х больше 2) -- значит в этой области корней нет.
2. х-1 меньше нуля, то есть х меньше 1.
в этом случае скобки обоих модулей снимаются с умножением выражений в скобках на минус единицу:
-х+1+х-2=1
иксы сокращаются:
-1=1 -- противоречие -- в этой области (х меньше 1) корней тоже нет.
3. х-1 больше или равно нуля а (х-2) меньше нуля,
то есть 1 меньше или равно х меньше 2
В этом случае скобки модуля х-1 просто убираются (снимаются)
а скобки модуля х-2 снимаются с умножением выражения в х-2 на минус единицу:
х-1+х-2=1
2х=4
х=2 -- не входит в область определения 1 меньше или равно х меньше 2
следовательно в третьем случае корней тоже нет.
ответ: Нет корней.