Объяснение:
Любой многочлен степени n вида  представляется произведением постоянного множителя при старшей степени  и n линейных множителей , i=1, 2, …, n, то есть , причем , i=1, 2, …, n являются корнями многочлена.
Эта теорема сформулирована для комплексных корней , i=1, 2, …, n и комплексных коэффициентов , k=0, 1, 2, …, n. Она является основой для разложения любого многочлена на множители.
Если коэффициенты , k=0, 1, 2, …, n – действительные числа, то комплексные корни многочлена ОБЯЗАТЕЛЬНО будут встречаться комплексно сопряженными парами.
К примеру, если корни  и  многочлена  являются комплексно сопряженными, а остальные корни действительные, то многочлен представится в виде , где 
По смыслу задачи в ящике остаются любые 100-90=10 носков. Тогда, эти носки могут быть и одного цвета. Но гарантируется, что хотя бы один носок каждого цвета извлечен. Тогда, носков каждого цвета должно быть хотя бы 11, чтобы в худшем случае 10 из них остались в ящике, а 1 был извлечен.
Теперь оценим, какое наибольшее количество носков одного цвета может быть. Для этого предположим, что носков всех цветов, кроме одного, то есть четырех цветов, содержится в минимально возможном количестве, то есть по 11. Тогда, носков последнего цвета окажется:
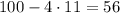
Тогда, в худшем случае, сначала из ящика будут извлечены эти 56 носков одного цвета, но 57-й носок гарантированно будет другого цвета.
ответ: 57