Переведем все значения в градусы, чтобы было привычнее.
π=180°
/ - так обозначается черта дроби.
переведу число -0,5 в дробь, тоже для удобства = -1/2
sin(180°/4-a) если cos a = -1/2 ; 180°/2<a<180°
sin(45°-a) если cos a= -1/2;
90<a<180° по условию угол находится во второй четверти. Синус в этой четверти принимает только положительные значения.
Как найти sin a? Вспомним основное тригонометрическое тождество:
cos²a+sin²a=1, отсюда выразим наш синус:
sin²a= 1-cos²a.
Чтобы найти sin a, возведем в корень 1-cos²a
Получаем: sin a = √1-cos²a.
Подставляем известное нам выражение cos a, которое мы не забываем возвести в квадрат.
sin a = √1-(-1/4) = √1+1/4 = √5/4 = √5/2
sin(45°-a)=sin45°cosa-cos45°sina= √2/2*(-1/2)-√2/2*√5/2=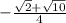 
Помним, что синус во второй четверти положительный.
Получаем ответ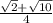 
-3.
Объяснение:
√(6 -2√5) - √(9+4√5) =
Заметтм, что каждое подкоренное выражение можно представить в виде квадрата суммы или разности:
6 -2√5 = 5 -2√5 + 1 = (√5)^2 -2•√5•1 + 1^2 =
(√5 -1)^2.
9 + 4√5 = 5 + 4√5 + 4 = (√5)^2 + 2•√5•2 + 2^2 =
(√5 + 2)^2.
Именно поэтому решение запишется так:
√(6 -2√5) - √(9+4√5) = √(√5 -1)^2 - √(√5 + 2)^2 = l√5 - 1l - l√5 + 2l
Выражения, записанные под знаком модуля положительные, знак модуля опускаем, не меняя знаки слагаемых в скобках:
(√5 - 1) - (√5 + 2) =
Упрощаем получившееся выражение:
√5 - 1 - √5 - 2 = -1 -2 = -3.
ответ: -3.
Использованные тождества:
а^2 - 2аb + b^2 = (a-b)^2;
а^2 + 2аb + b^2 = (a+b)^2;
√(a)^2 = lal.
x^4-1-4x²+56=0
x^4-4x²+55=0
Пусть x²=t
t²-4t+55=0
D=16-220=-204<0
Нет корней.
ответ:Нет корней.