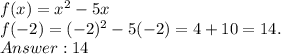
Псть скорость туриста из А равна х. Тогда скорость второго равна х-1. Если первый турист шел а часов, то второй - а+0,5.Составляем систему:
а*х=9 (расстояние, которое первый турист до встречи); (а+0,5)(х-1)=10 (расстояние второго до встречи)
Второ выражение:
(а+0,5)(х-1)=10
а = 10/(х-1) - 0,5 = 10/(х-1) - 1/2 = (21-х)/(2х-2)
Подсталяем в первое уравнение значение а:
а*х = 9
(21-х)/(2х-2) * х = 9
(21-х)х=9(2х-2)
21х-х^218х-18
х^2-3х-18 = 0
Дискриминант= 9+4*18 = 81
х1=-6 - не подходит
х2=3
Скорость туриста из пункта А равна 3км/ч
Пусть х км/ч скорость туриста, вышедшего из В, тогда скорость туриста, вышедшего из А х+1 км/ч. Турист вышедший из А потратил 9/(х+1) + 1/2 часов, а турист , вышедший из В, потратил 10/х. Составим и решим уравнение:
9/(х+1) + 1/2 = 10/х
переносим все в левую часть, приводим к общему знаменателю, и должно получится примерно следующее:
(х²-х-20)/(2х(х+1)) ОДЗ: х≠0, -1
решаем квадратное уравнение:
D=1+80=81=9²
корни уравнения : 5 и -4 (-4 не подходит по смыслу задачи)
Значит, скорость вышедшего из В равна 5 км/ч, тогда скорость туриста, вышедшего из А, равна 5+1 = 6км/ч
ответ: 6 км/ч